|
Responeu a QUATRE de les sis qüestions següents. En les respostes, expliqueu sempre què voleu fer i per què.
1- Considereu la funció polinòmica `f(x) = 3x^13 + 5x^3 + 2`. a) Justifiqueu que la seva gràfica talla l’eix de les abscisses en un punt de l’interval `[–2, 0]`. Doneu un interval de longitud `0,5` on es trobi aquest punt de tall. [1,25 punts] b) Estudieu les zones de creixement i de decreixement, i els màxims i els mínims de `y = f(x)`. Quants punts de tall té exactament la gràfica d’aquesta funció amb l’eix de les abscisses? Justifiqueu la resposta. [1,25 punts] SOLUCIÓ 2- Considereu el sistema d’equacions següent, on `m` és un paràmetre real: $$ \begin{cases} x-3y+mz=-2\\ x+my+2z=3\\ x+y+2z=m \end{cases} $$ a) Discutiu el sistema segons el valor del paràmetre `m`. [1,25 punts] b) Trobeu la solució del sistema per a `m = 0`. [0,5 punts] c) Per a `m = 2`, doneu una solució `(x, y, z)` del sistema que, a més a més, compleixi `x = 5y`. [0,75 punts] 3- La classe de l’Èlia ha dissenyat el logotip següent per a pintar-lo a la paret de l’institut: 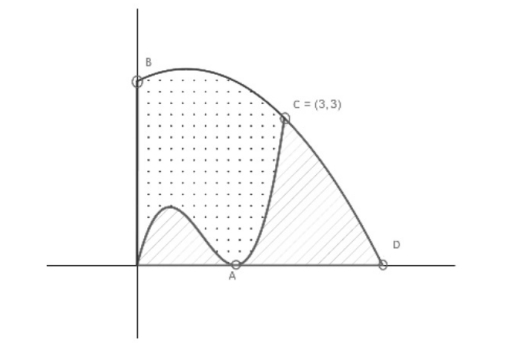 La corba que passa pel punt `A` és `y = f(x)`, amb `f(x) = x^3 – 4x^2 + 4x`, i la que passa pels punts `B`, `C = (3, 3)` i `D` és `y = g(x)`, amb `g(x)=-((x-1)/2)^2+4`. a) Calculeu les coordenades dels punts `A`, `B` i `D`. [0,75 punts] b) Calculeu l’àrea de la zona puntejada. [1,25 punts] c) Els alumnes volen pintar la part puntejada de color blau i la part ratllada de color vermell. Sabent que l’àrea total del logotip és `175/12` `m^2` , de quin color necessitaran més pintura? [0,5 punts] SOLUCIÓ 4- S’estima que el `20 %` dels habitants d’una regió pateix algun tipus d’arrítmia. Per a diagnosticar-la, hi ha la possibilitat de col·locar al pacient un monitor Holter, que detecta l’arrítmia en un `95 %` dels casos de persones que la pateixen, però que també dona falsos positius, per motius elèctrics, en persones que no pateixen arrítmies en un `0,5 %` dels casos. a) Si escollim `4` persones a l’atzar, quina és la probabilitat que almenys una d’elles pateixi arrítmies? [0,75 punts] b) Quina és la probabilitat que una persona escollida a l’atzar obtingui un diagnòstic positiu d’arrítmia? [0,75 punts] c) Si una persona obté un diagnòstic negatiu a la prova del Holter, quina és la probabilitat que realment pateixi arrítmies? [1 punt] 5- Per a cada punt `(x, y)` de la corba `y = e^(–2x)`, amb `x > 0` i `y > 0`, considereu el rectangle amb vèrtexs als punts `(0, 0)`, `(x, 0)`, `(0, y)` i `(x, y)`. a) Comproveu que, d’entre tots aquests rectangles, el que té `x=1/2` és el d’àrea màxima. Quin és el valor d’aquesta àrea? [1,5 punts] b) Calculeu l’equació de la recta tangent a la funció `y = e^(–2x)` en el punt d’abscissa `x = 0`, i el seu punt de tall amb l’eix de les abscisses. [1 punt] SOLUCIÓ 6- Considereu el punt `P = (1, 3, 0)` i el pla `\pi` d’equació `x + 2y – 2z = –7`. a) Sigui `r` la recta que és perpendicular a `\pi` i passa per `P`. Calculeu el punt d’intersecció de `\pi` amb `r`. [1 punt] b) Calculeu la distància `d` del punt `P` al pla `\pi`. [0,5 punts] c) Calculeu l’equació d’un altre pla `\pi'` que sigui paral·lel a `\pi` i que també estigui a distància `d` de `P`. [1 punt] |