(2024-setembre-1-5) Per a cada punt `(x, y)` de la corba `y = e^(–2x)`, amb `x > 0` i `y > 0`, considereu el rectangle amb vèrtexs als punts `(0, 0)`, `(x, 0)`, `(0, y)` i `(x, y)`. a) Comproveu que, d’entre tots aquests rectangles, el que té `x=1/2` és el d’àrea màxima. Quin és el valor d’aquesta àrea? [1,5 punts] b) Calculeu l’equació de la recta tangent a la funció `y = e^(–2x)` en el punt d’abscissa `x = 0`, i el seu punt de tall amb l’eix de les abscisses. [1 punt] Solució: 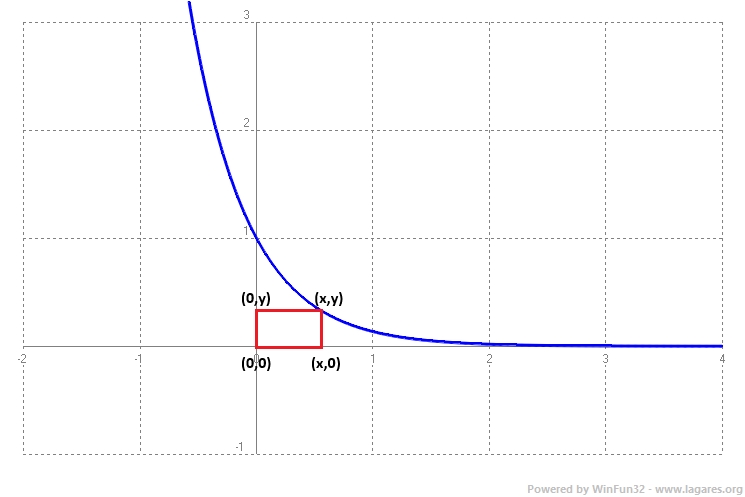a) Fem un dibuix que ens ajudarà a aclarir de què va tot plegat. La funció àrea en funció de `x` és base · altura. La base és `x` i l'altura, `y=e^(-2x)`. Per la qual cosa l'àrea és: `A(x)=x·e^(-2x)` Per trobar-ne els extrems calcularem la derivada: `A'(x)=e^(-2x)+xe^(-2x)·(-2)=(1-2x)e^(-2x)` Si ho igualem a `0`. `(1-2x)e^(-2x)=0 => (1-2x)=0 => x=1/2`. Ja que la funció exponencial sempre és positiva, mal val `0` Per veure que és un màxim calculem les derivades a la dreta i l'esquerra (recorem que `A'(x)` és contínua i no té asímptotes i l'únic punt de tall amb l'eix d'abscises és `x=1/2`. `A'(0)=(1-2·0)e^(-2·0)=1>0` a l'esquerra la funció és creixent. `A'(1)=(1-2·1)e^(-2·1)=-1·e^(-2)<0` ja que `e^x` és sempre positiva `=>` a la dretala funció és decreixent. Per la qual cosa, en el punt, `x=1/2` la funció àrea té un màxim. I el valor de l'àrea és: `A(1/2)=1/2·e^(-2·1/2)=1/2·e^(-1)=1/(2e)` `u^2` b) Calculem la derivada de la funció `y=e^(-2x) => y'=-2·e^(-2x)` la calculem a `y'(0)=-2e^(-2·0) => y'(0)=-2` que és el pendent. Calculem la imatge de `x=0 => y(0)=e^(-2·0)=e^0=1`. O sigui cal calular l'equació de la recta que passa per: `(0,1)` i té de pendent `m=-2 =>` `y-y_0=m(x-x_0)` `y-1=-2(x-0)` `y-1=-2x` `y=-2x+1` Finalment ens demanen el punt de tall d'aquesta recta amb l'eix d'abscises. recta d'equació, `y=0`. Ho substituïm: `0=-2x+1` `-1=-2x` `x=1/2` `(1/2,0)` El problema no ho demana, però dibuixem la funció i la recta demanada i queda: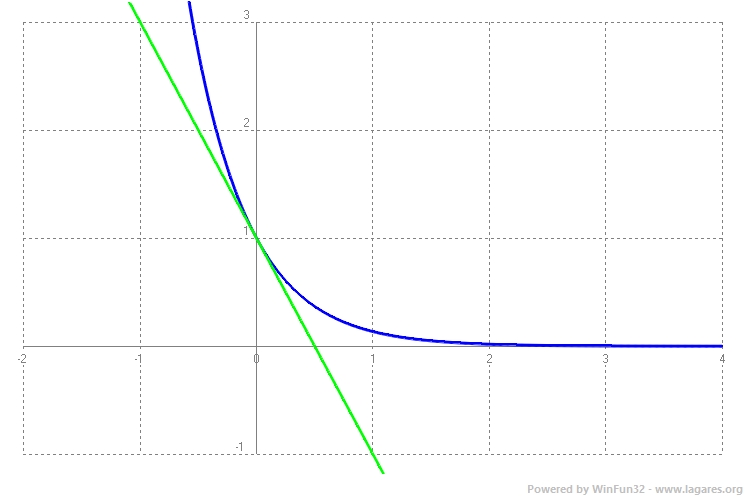