(2024-setembre-1-3) La classe de l’Èlia ha dissenyat el logotip següent per a pintar-lo a la paret de l’institut:
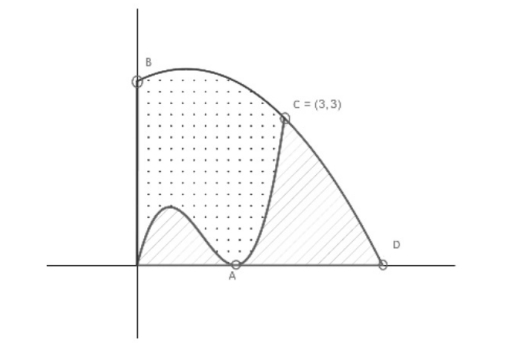
La corba que passa pel punt `A` és `y = f(x)`, amb `f(x) = x^3 – 4x^2 + 4x`, i la que passa pels punts `B`, `C = (3, 3)` i `D` és
`y = g(x)`, amb `g(x)=-((x-1)/2)^2+4`.
a) Calculeu les coordenades dels punts `A`, `B` i `D`.
[0,75 punts]
b) Calculeu l’àrea de la zona puntejada.
[1,25 punts]
c) Els alumnes volen pintar la part puntejada de color blau i la part ratllada de color vermell. Sabent que l’àrea total del logotip és `175/12` `m^2`, de quin color necessitaran més pintura?
[0,5 punts]
Solució:
a)
- Per trobar `A` cal trobar els punts de tall de `f(x)=x^3-4x^2+4x` amb l'eix d'abscisses:
`x^3-4x^2+4x=0`
`(x^2-4x+4)x=0` que té la solució `x=0` que ja veiem a la gràfica. Cerquem les altres arrels:
`x^2-4x+4=0`
`x=(4\pm\sqrt{(-4)^2-4·1·4})/2=(4\pm\sqrt{0))/2=2`
`A=(2,0)`
- Per trobar `B` cal trobar la imatge de `x=0` per la funció `g(x)=-((x-1)/2)^2+4`
`g(0)=-((0-1)/2)^2+4=-1/4+4=15/4`
`B=(0,15/4)`
- Per trobar `D` cal trobar el punt de tall de la funció `g(x)=-((x-1)/2)^2+4` amb l'eix d'abcisses:
`-((x-1)/2)^2+4=0`
`-((x-1)/2)^2=-4`
`((x-1)/2)^2=4`
`\sqrt{((x-1)/2)^2}=\sqrt{4}`
`(x-1)/2=\pm2`
`x-1=\pm4`
`x=\pm4+1 => x_1=5` i `x_2=-3` Ens quedem amb `x_1=5` perquè estudiem la part positiva de `g(x)`
`D=(5,0)`
b)
Per trobar l'àrea de la zona puntejada cal trobar la integral definida entre `0` i `3` de `g(x)-f(x)`.
En primer lloc escriurem `g(x)` d'una altra manera:
`g(x)=-((x-1)/2)^2+4=-1/4(x^2-2x+1)+4=-x^2/4+x/2-1/4+4=-x^2/4+x/2+15/4`
Àrea `=`
`\int_0^3 [(-x^2/4+x/2+15/4)-(x^3 – 4x^2 + 4x)] dx= \int_0^3 [-x^2/4+x/2+15/4-x^3 + 4x^2 - 4x]dx=`
`\int_0^3 [-x^3+ 4x^2-x^2/4+x/2 - 4x+15/4]dx = \int_0^3 [-x^3+ (15x^2)/4-(7x)/2+15/4]dx=`
`[-x^4/4+(15x^3)/12-(7x^2)/4+15/4x]_0^3=(-3^4/4+(15·3^3)/12-(7·3^2)/4+15/4·3)-0=9` `u^2`
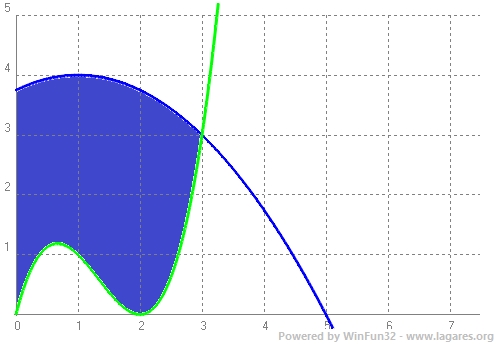
c)
Per trobar l'àrea ratllada calcularem l'àrea sota la funció `g(x)` i els eixos i li restarem l'àrea trobada.
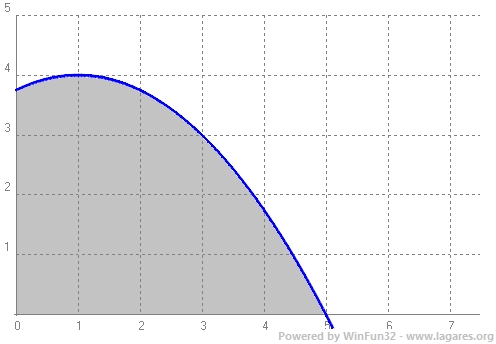
`\int_0^5 (-x^2/4+x/2+15/4) dx =[-x^3/12+x^2/4+15/4x]_0^5=(-5^3/12+5^2/4+15/4·5)-0=14,58333`
Que si li restem, `14,58333-9 = 5,58333` `u^2` és l'àrea de la part ratllada:
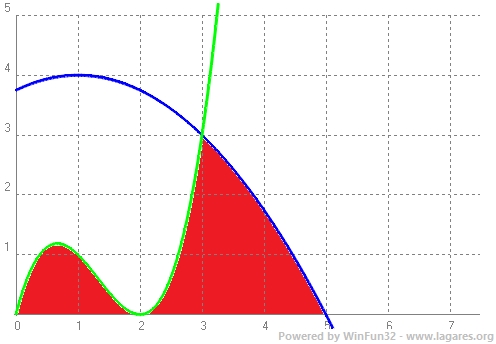
L'àrea de la part puntejada és `9` `u^2` la de la part ratllada `5,58333` `u^2` Per la qual cosa l'àrea de la part puntejada és més gran.
c')
Dins l'enunciat ens diuen que l'àrea de tot el logotip (àrea sota la funció `g(x)` i els eixos) val `175/12 = 14,58333`. O sigui ja ens donaven l'àrea sota la corva, per la qual cosa no calia calcular la integral. Però així hem tancat millor el problema. Així hi tot l'enunciat portava una ambigüitat, ja que ens donava aquest `175/12` en `m^2` i no parlava de que les unitats dels eixos fossin `m` (metres).
Amb això la solució de l'apartat c) era molt més curta Àrea part ratllada `=175/12-9 = 5,583333` que evidentment és més petita que `9` àrea de la part ratllada.
|



