(2024-setembre-1-1) Considereu la funció polinòmica `f(x) = 3x^13 + 5x^3 + 2`. a) Justifiqueu que la seva gràfica talla l’eix de les abscisses en un punt de l’interval `[–2, 0]`. Doneu un interval de longitud `0,5` on es trobi aquest punt de tall. [1,25 punts] b) Estudieu les zones de creixement i de decreixement, i els màxims i els mínims de `y = f(x)`. Quants punts de tall té exactament la gràfica d’aquesta funció amb l’eix de les abscisses? Justifiqueu la resposta. [1,25 punts] Solució: a) La funció és polinòmica que és continua de `(-\infty, \infty)` per la qual cosa, si veiem que `f(-2)` té signe contrari de `f(0)` pel teorema de Bolzano podem assegurar que hi ha una arrel entre els dos punts. `f(-2)=3*(-2)^13+5*(-2)^3+2 = -24614`           i           `f(0)=2` Si cerquem les imatges de `{-1,5; -1; -0,5}` i veiem entre quins valors la funció canvia de signe, tindrem l'arrel acotada entre els dos valors. `f(-1,5)=3*(-1,5)^13+5*(-1,5)^3+2 = -598,733520507813` `f(-1)=3*(-1)^13+5*(-1)^3+2 = -6` `f(-0,5)=3*(-0,5)^13+5*(-0,5)^3+2 = 1,374633` Com que `f(-1)·f(-0,5)<0 =>` que l'arrel està entre `(-1;-0,5)` b) Calculem la primera derivada per trobar el creixement-decreixement i/0 els extrems: `f'(x)=39x^12+15x^2` A partir d'aquí podem fer el raonament de dues maneres: b_1) Com els exponnts de la `x` són parells la derivada no pot ser mai negativa, per la qual cosa la funció sempre és creixent i no hi pot haver-hi ni màxims, ni mínims. En ser una funció polinòmica no té ni asímptotes ni discontinuïtats per la qual cosa només pot tenir un punt de tall que es troba a l'interval `(-1;-0,5)` b_2) Trobant els extrems. O igualem a `0` `39x^12+15x^2=0` `(39x^10+15)x^2=0` Aquesta equació pot tenir dues solucions, `x^2=0 => x=0`      i       `39x^10+15=0 => x=\root(10){-15/39}` que no té cap solució real, ja que és una arrel parell d'un nobre negatiu. L'únic candidat a ser extrem és `x=0` Calclem la segona derivada i substituïm, `f''(x)=468x^11+30x` que si substituïm per `0 => f''(0)=0 =>` Que pot no ser un extrem, pot ser un punt d'inflexió. Calculem la tercera derivada, `f'''(x)=468·11x^10+30 => f'''(0)=30 \ne 0 =>` a `x=0` hi ha un punt d'inflexió. Com la funció no té cap extrem, ni màxims, ni mínims, i la funció és contínua, semre serà creixent o decreixent, per veure si és una cosa o l'altre podem substituir qualsevolvalor a la primera derivada, menys el `0` que hi ha un punt d'inflexió i mirar si és positiva o negativa. `f'(1)=39*1^12+15*1^2 = 54 > 0 =>` la funció és sempre creixent. Com la funció sempre és creixent només pot tenir un punt de tall, que és el que està entre `(-1;-0,5)` El problema no ho demana, però oferim la gràfica de la funció per visualitzar tot el que hem comentat: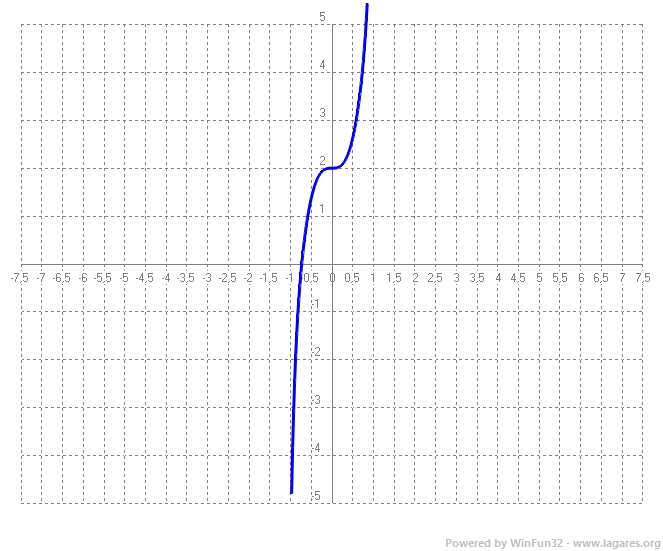