GEOMETRIA



-(2024-juny-1-6) Considereu els punts `A = (1, 2, 3)` i `B = (–3, –2, 3)`.

a) Calculeu l’equació del pla `pi` que és perpendicular a la recta `AB` i que passa pel punt mitjà entre `A` i `B`. Justifiqueu ue aquest pla està format, precisament, pels punts `P = (x, y, z)` que estan a igual distància de `A` que de `B`, és a dir, `d(P, A) = d(P, B)`. [1 punt]

b) Calculeu les distàncies de A i de B al pla p i comproveu que són iguals. És casualitat? Raoneu la resposta. [0,75 punts]

c) Sigui `C = (–7, 6, 3)`. El triangle `ABC` és isòsceles? Calculeu la seva àrea. [0,75 punts]


SOLUCIÓ



-(2023-juny-1-6) Siguin els plans `pi_1` i `pi_2`, determinats respectivament per les equacions `pi_1: x + y = 3` i `pi_2: x – z = –2`.

    a)Trobeu l’equació general `(Ax + By + Cz + D = 0)` del pla `pi_3`, que és perpendicular a `pi_1` i `pi_2`, i que passa pel punt `P = (4, 1, 2)`. [0,75 punts]

    b)Sigui `r` la recta d’intersecció de `pi_1` i `pi_2`. Calculeu l’equació vectorial de la recta `r`. [0,75 punts]

    c)Calculeu el punt `Q` de la recta `r` que és més a prop del punt `P`. [1 punt]

SOLUCIÓ



-(2023-setembre-2-5) Siguin `r_1` i `r_2` les rectes definides per `r_1: x – 1 = y = –z` i per `r_2: x = y = z`, respectivament.

    a) Calculeu l’equació paramètrica de la recta que talla perpendicularment les rectes `r_1` i `r_2`. [1,75 punts]

    b) Calculeu la distància entre `r_1` i `r_2`. [0,75 punts]

SOLUCIÓ


-(2022-juny-2-3)- Sigui la recta `r` definida per l’expressió següent:
$$
r:\begin{cases}
x=2+\lambda\\
y=-1+3\lambda\\
z=3+\lambda
\end{cases}
$$
    a) Determineu la posició relativa de la recta `r` respecte al pla `pi: x – 2y + 4z – 4 = 0`. Si és paral·lela, calculeu la distància de `r` a `pi`, i si és secant, calculeu el punt de tall. [1,25 punts]

    b) Calculeu l’equació de la recta s perpendicular al pla `pi` i que talla la recta `r` en un punt `P`, la primera coordenada del qual és `5` vegades més gran que la segona. [1,25 punts]

SOLUCIÓ



-(2022-setembre-3-1)- El pal central que sosté la lona de la carpa d’un circ se situa perpendicularment sobre el pla d’un terra l’equació del qual és `pi: x – z = 6`. Sabem que la cúpula de la carpa (el punt més alt per on passa el pal) és al punt de coordenades `P = (30, 1, 0)`.

    a) Calculeu l’equació paramètrica de la recta que conté el pal. [1 punt]

    b) Calculeu les coordenades del punt de contacte del pal amb el terra, i la longitud del pal. [1,5 punts]

SOLUCIÓ



-(2021-juny-2-3). Considereu el punt `P = (–1, 3, 1)`, el pla `pi : x = y` i la recta `r:(x-1)/2=y/3=z-2`.

    a) Trobeu les coordenades del punt `P'` simètric a `P` respecte al pla `pi`. [1,25 punts]

    b) De tots els plans que contenen la recta `r`, trobeu l’equació cartesiana del que és perpendicular al pla `pi`. [1,25 punts]

SOLUCIÓ



-(2021-setembre-1-3). En `R^3` es donen els punts `A = (3, 1, 1)`, `B = (0, 0, 1)`, `C = (4, 1, 2)` i `D = (1, 1, t)`, en què `t` és un valor real.

a) Per a quin valor de t els quatre punts són coplanaris? [1 punt]

b) Trobeu el valor de `t` per tal que el tetraedre (irregular) que formen els quatre punts tingui un volum de `5` `u^3` [1,5 punts]

Nota: El volum d’un tetraedre definit pels vectors `v_1`, `v_2` i `v_3` és igual a un sisè del valor absolut del determinant de la matriu formada per tots tres vectors,

`V=1/6|det(V_1,V_2,V_3)|`

SOLUCIÓ



-(2020-juny-1-3) a) Calculeu l'equació general del pla `pi` que passa pel punt `(8, 8, 8)` i té com a vectors directors `u = (1, 2, -3)` i `v = (-1, 0, 3)`.

b) Determineu el valor del paràmetre `a` perquè el punt `(1, -5, a)` pertanyi al pla `pi` i cal­culeu l'equació paramètrica de la recta que passa per aquest punt i és perpendicular al pla `pi`.

SOLUCIÓ



-(2020-juny-3-5) Considereu la recta `r` d'equació `(x-1)/2=(y-3)/(-2)=z/1` i la recta `s` que passa pel punt `P = (2, -5, 1)` i que té per vector director `(-1, 0, -1)`.
    a) Estudieu la posició relativa de les rectes `r` i `s`.

    b) Calculeu l'equació general del pla que és paral·lel a la recta `r` i conté la recta `s`.

SOLUCIÓ



-(2020-setembre-4-2) Un avió es desplaça des d'un punt `A = (0, 3, 1)` cap a una plataforma plana d'equació `pi: x - 2y + z = 1` seguint una recta `r` paral·lela al vector `v = (1, -1, 0)`.
    a) Calculeu les coordenades del punt de contacte `B` de l'avió amb el pla i la distància recorreguda.

    b) Calculeu l'equació general del pla perpendicular a la plataforma i que conté la recta `r` seguida per l'avió des del punt `A`.
SOLUCIÓ


-(2020-setembre-4-6) Siguin les rectes `r` i `s`, expressades per `(x-3)/2= y = z - 1` i `(mu, -mu, mu)`, respectivament.
    a) Determineu la posició relativa de les rectes.

    b) Calculeu la distància entre la recta `r` i la recta `s`.
SOLUCIÓ




-(2019-juny-1-3)Un dron es troba en el punt `P = (2, -3, 1)` i volem dirigir-lo en línia recta fins al punt més proper del pla d'equació `pi : 3x + 4z + 15 = 0`.
    a) Calculeu l'equació de la recta, en forma paramètrica, que ha de seguir el dron. Quina distància ha de recórrer fins a arribar al pla?

    b) Trobeu les coordenades del punt del pla on arribarà el dron.

Nota: Podeu calcular la distància que hi ha d'un punt de coordenades `(x_0, y_0, z_0)` al pla d'equació `Ax + By + Cz + D = 0` amb l'expressió `|Ax_0+By_0+Cz_0+D|/sqrt(A^2+B^2+C^2)`

SOLUCIÓ



-(2019-juny-4-2) Siguin la recta:
$$
r:\begin{cases} x=2\\
y-z=1 \end{cases}
$$
i el pla `pi:x-z=3`
    a) Calculeu l'equació paramètrica de la recta que és perpendicular al pla `pi` i que el talla en el mateix punt en què el talla la recta `r`.

    b) Trobeu els punts de `r` que estan a una distància de `sqrt(8)` unitats del pla `pi`

Nota: Podeu calcular la distància que hi ha d'un punt de coordenades `(x_0, y_0, z_0)` al pla d'equació `Ax + By + Cz + D = 0` amb l'expressió `|Ax_0+By_0+Cz_0+D|/sqrt(A^2+B^2+C^2)`

SOLUCIÓ




-(2019-juny-4-5) Considereu els plans `pi_1: 2x + ay + z = 5`, `pi_2: x + ay + z = 1` i `pi_3: 2x + (a + 1)y + (a + 1)z = 0`, en què `a` és un paràmetre real.
    a) Estudieu per a quins valors del paràmetre `a` els tres plans es tallen en un punt.

    b) Comproveu que per al cas `a = 1` la interpretació geomètrica del sistema format per les equacions dels tres plans és la que es mostra en la imatge següent: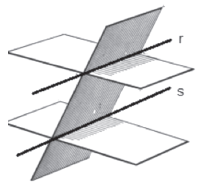

SOLUCIÓ



-(2019-setembre-5-5) Siguin `P`, `Q` i` R` els punts d'intersecció del pla d'equació `x + 4y + 2z = 4` amb els tres eixos de coordenades `OX`, `OY` i `OZ`, respectivament.
    a) Calculeu els punts `P`, `Q` i `R`, i el perímetre del del triangle de vèrtexs `P`, `Q` i `R`.

    b) Calculeu l'àrea del triangle de vèrtexs `P`, `Q` i `R`.
Nota: Per a calcular l'àrea del triangle definit pels vectors `v` i `w` podeu fer servir l'expressió `S=1/2 |v` x `w|` , en què `v` × `w` és el producte vectorial dels vectors `v` i `w`.

SOLUCIÓ