|
L’examen consta de QUATRE exercicis obligatoris. Cada exercici val 2,5 punts. Feu els exerci-cis 1, 2 i 3 responent a TOTES les qüestions que s’hi plantegen. A l’exercici 4, trieu UNA de les dues opcions (A o B) proposades. En totes les respostes, expliqueu sempre què voleu fer i per què. Cal que la redacció de la resposta es faci de manera coherent, amb correcció i claredat, emprant la notació i el vocabulari matemàtic adequats i expressant la solució de manera clara. Podeu utilitzar les pàgines en blanc del final del quadern per a fer esquemes, esborranys, etc., o per a acabar de respondre a algun exercici si necessiteu més espai. En aquest últim cas, cal que ho indiqueu clarament al final de la pàgina de l’exercici corresponent. Podeu utilitzar calculadora, però no es permet l’ús de calculadores o altres aparells capaços d’emmagatzemar dades o de transmetre o rebre informació. 1-Una família vol comprar un terreny per a fer-s’hi una casa envoltada de penya-segats amb vistes al mar. En aquella zona de la costa, els penya-segats segueixen les rectes `y = 0` i `y = 3x`. A més, la família vol que el terreny sigui triangular i que el tercer costat del triangle passi pel punt `P = (1, 1)`, tal com es pot veure en la figura. 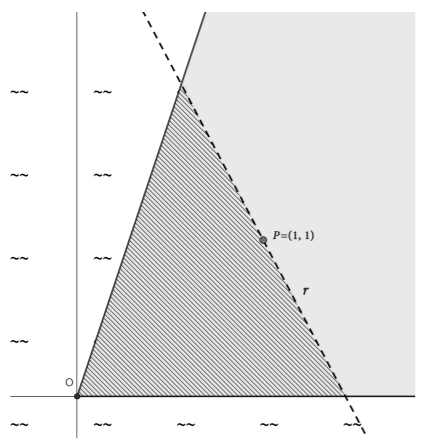 a) Plantegeu l’equació de la recta r que defineix el tercer costat del triangle en funció del seu pendent `m`, i comproveu que l’àrea del terreny ve donada per `A(m)=3/2·(m^2-2m+1)/(m^2-3m)`. [1 punt] b) Calculeu el valor de `m` que fa que l’àrea d’aquest terreny (i, per tant, el seu preu) sigui mínima. Quin és el valor d’aquesta àrea? [1,5 punts] SOLUCIÓ 2-Considereu el sistema d’equacions lineals següent: $$ \begin{cases} x+3y+z=5\\ mx+2z=0\\ my-z=m \end{cases} $$ a) Discutiu el sistema per als diferents valors del paràmetre `m`. [1,25 punts] b) Resoleu el sistema per a `m = 1`. [0,5 punts] c) Resoleu el sistema quan aquest tingui infinites solucions. [0,75 punts] 3-La lesió per sesamoïditis (inflamació de l’os sesamoide del peu) és relativament habitual entre la població que practica esports d’impacte (atletisme, bàsquet, tennis…). En una pobla-ció d’esportistes, s’ha fet un estudi diferenciant entre els que practiquen esports d’impacte i els que practiquen esports sense impacte brusc (com ara natació, pilates, senderisme…). S’ha pogut determinar que el `45 % ` practiquen esports d’impacte. Entre aquests, un `10 %` pateixen lesions per sesamoïditis, mentre que entre els que no practiquen esports d’impacte només un `3 %` presenten aquesta lesió. Escollim un esportista a l’atzar. a) Quina és la probabilitat que pateixi sesamoïditis? [0,75 punts] b) Si l’esportista escollit té una lesió per sesamoïditis, quina és la probabilitat que practiqui esports d’impacte? [0,75 punts] Una empresa de calçat esportiu ha creat una sabatilla amb amortiment per a minimitzar les lesions per sesamoïditis. Els beneficis generats per la venda d’aquest producte, en milers d’euros, segueixen una funció de la forma `f(x) = ax3 + bx2 + cx`, on `x` són els anys transcorreguts des que la sabatilla va sortir a la venda i `a`, `b` i `c` són constants reals. c) Calculeu els valors de `a`, `b` i `c` sabent que el primer any es van obtenir el màxim de beneficis, amb un valor de `8 000` euros, i que el segon any va haver-hi un punt d’inflexió en els beneficis. [1 punt] 4-Trieu UNA de les dues opcions (A o B) i responeu a les qüestions que s’hi plantegen. OPCIÓ A Un vidrier està reparant un dels vitralls de la Sagrada Família la forma del qual és la de la part ombrejada de la figura adjunta. S’ha adonat que Gaudí el va dissenyar de manera que un dels costats segueix la funció `y = 3sin(x/4)` i un altre segueix la funció ` y = 3cos(x/4)`, on `x` i `y` estan expressades en metres. 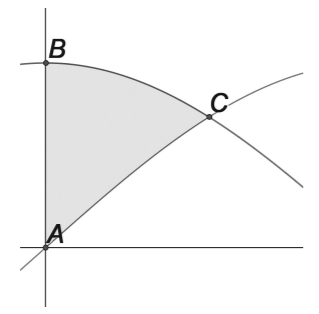 a) Raoneu a quina funció correspon cada gràfica i calculeu les coordenades dels punts `B` i `C` assenyalats a la figura (tenint en compte que A és l’origen de coordenades). [1 punt] b) Calculeu el preu del vitrall sabent que costa `750` €/`m^2`. [1,5 punts] SOLUCIÓ OPCIÓ B Considereu el pla `\pi: 2x – y + z = 5` i el punt `P = (0, 1, 3)`. a) Comproveu que la distància del punt `P` al pla `\pi` és `\sqrt{6}/2`. [0,5 punts] b) Trobeu l’equació general d’un pla `\pi_1` para?lel a `\pi` i que passi pel punt `P`. Quina és la distància entre `\pi_1` i `\pi`? [0,75 punts] c) Trobeu l’equació general d’un segon pla `\pi_2`, diferent de `\pi_1`, que és paral·lel a `\pi` i que estigui a una distància `\sqrt{6}/2` de `\pi`. [1,25 punts] |