-(2025-setembre-1-1) Una família vol comprar un terreny per a fer-s’hi una casa envoltada de penya-segats amb vistes al mar. En aquella zona de la costa, els penya-segats segueixen les rectes `y = 0` i `y = 3x`. A més, la família vol que el terreny sigui triangular i que el tercer costat del triangle passi pel punt `P = (1, 1)`, tal com es pot veure en la figura.
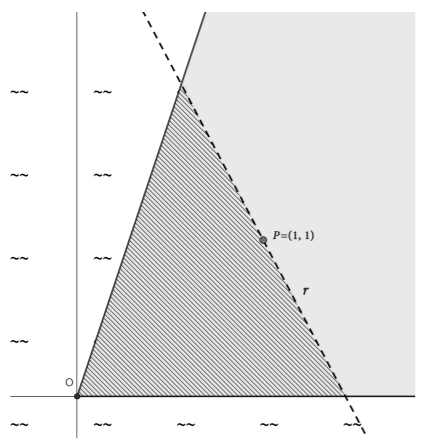
a) Plantegeu l’equació de la recta r que defineix el tercer costat del triangle en funció del seu pendent `m`, i comproveu que l’àrea del terreny ve donada per `A(m)=3/2·(m^2-2m+1)/(m^2-3m)`.
[1 punt]
b) Calculeu el valor de `m` que fa que l’àrea d’aquest terreny (i, per tant, el seu preu) sigui mínima. Quin és el valor d’aquesta àrea?
[1,5 punts]
Solució:
a)
`y-1=m(x-1)`
`y-1=mx-m`
`y=mx-m+1`
- Per trobar l'àrea cal que trobem la `y` de la intersecció amb la recta, `y=3x`, que és l'altura del triangle.
`y=3x => y/3=x`. Ho substituim a l'equació de l'altra recta.
`y=my/3-m+1`
`3y=my-3m+3`
`3y-my=-3m+3`
`(3-m)y=-3m+3`
`y=(-3m+3)/(3-m)`
- I per trobar la base del triangle cal trobar la intersecció, la `x` amb l'eix d'abscises, `y=0`
`0=mx-m+1`
`m-1=mx`
`(m-1)/m=x`
- Finalment, per trobar l'àrea `(\text{base} · \text{altura})/2 => (x·y)/2`
`(m-1)/m·(-3m+3)/(3-m)·1/2=(-3m^2+3m+3m-3)/(2(3m-m^2))=(-3m^2+6m-3)/(2(3m-m^2))=(3m^2-6m+3)/(2(m^2-3m))=3/2·(m^2-2m+1)/(m^2-3m)`
Àrea=`3/2·(m^2-2m+1)/(m^2-3m) =A(m)`
b)
- Per trobar el mínim derivarem la funció i l'igualarem a `0` per trobar els extrems relatius.
`A'(m)=3/2·((2m-2)·(m^2-3m)-(m^2-2m+1)·(2m-3))/(m^2-3m)^2`
`A'(m)=3/2·(2m^3-6m^2-2m^2+6m -(2m^3-3m^2-4m^2+6m+2m-3))/(m^2-3m)^2`
`A'(m)=3/2·(2m^3-6m^2-2m^2+6m -2m^3+3m^2+4m^2-6m-2m+3)/(m^2-3m)^2`
`A'(m)=3/2·(-m^2-2m+3)/(m^2-3m)^2`
Ho igualem a `0`. Que vol dir igualar a `0` el numerador.
`-m^2-2m+3=0`
`x=(2\pm\sqrt{(-2)^2-4·(-1)·3})/(-2)=(2\pm\sqrt{16})/(-2)=(2\pm4)/(-2) =>`, `x_1=-3` i `x_2=1`
- Per mirar si són màxims o mínims, calculem la segona derivada:
`A''(m)=3/2·((-2m-2)·(m^2-3m)^2-(-m^2-2m+3)·2·(m^2-3m)·(2m-3))/(m^2-3m)^4`
La resta del numerador val `0` per `m=1` i `m=-3`, ja que son les arrels del polinomi de segon grau de la seva factorització.
`A''(1)=3/2·((-2·1-2)·(1^2-3·1)^2)/(1^2-3·1)^4=3/2·(-16)/16=-3/2<0 =>` a `m=1` hi ha un màxim.
`A''(-3)=3/2·((-2·(-3)-2)·((-3)^2-3·(-3))^2)/((-3)^2-3·(-3))^4=3/2·(1296)/104976=3/2·1/81=1/54 >0 =>`
a `m=-3` hi ha un mínim.
- Finalment calculem l'àrea per a `m=-3` que serà quan el terreny sigui més barat.
`A(m)=3/2·(m^2-2m+1)/(m^2-3m)`
`A(-3)=3/2*((-3)^2-2*(-3)+1)/((-3)^2-3*(-3)) = 1,333333 = 4/3` `u^2`
|
