|
(2025-setembre-1-4A) Un vidrier està reparant un dels vitralls de la Sagrada Família la forma del qual és la de la part ombrejada de la figura adjunta. S’ha adonat que Gaudí el va dissenyar de manera que un dels costats segueix la funció `y = 3sin(x/4)` i un altre segueix la funció `y = 3cos(x/4)`, on `x` i `y` estan expressades en metres. 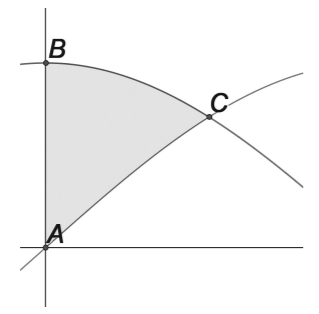 a) Raoneu a quina funció correspon cada gràfica i calculeu les coordenades dels punts `B` i `C` assenyalats a la figura (tenint en compte que A és l’origen de coordenades). [1 punt] b) Calculeu el preu del vitrall sabent que costa `750` €/`m^2`. [1,5 punts] Solució: a) La funció sinus passa pel `(0,0` per la qual cosa la funció que passa pel punt `A` és `y = 3sin(x/4)`. La funció cosinus passa pel punt `(1,0)` per la qual cosa la funció que passa pel punt `B` és `y = 3cos(x/4)` i el punt `B=(0,3)` Per trobar el punt `C` cal trobar el punt de tall més proper a l'eix `y` de les dues funcions: `3sin(x/4)=3cos(x/4)` `sin(x/4)=cos(x/4)` `sin(x/4)/cos(x/4)=1` `tan(x/4)=1` L'angle que la seva tangent val `1` és `\pi/4`. Això s'hauria de saber. O si no, podem calcular `arctan(1)=\pi/4` I per trobar la `y = 3sin(\pi/4)=(3\sqrt{2})/2 =>` b) Per calcular l'àrea demanada cal trobar: `\int_0^\pi (3cos(x/4)-3sin(x/4))dx=3\int_0^\pi (cos(x/4)-sin(x/4))dx=` `3[(4sin(x/4)+4cos(x/4)]_0^\pi=3·4[sin(\pi/4)+cos(\pi/4)-sin(0)-cos(0)]=12(\sqrt{2}/2+\sqrt{2}/2-0-1)=12(\sqrt{2}-1)` `\approx 4,97` `m^2` El problema no ho demana, però aquí teniu la gràfica del què hem calculat: 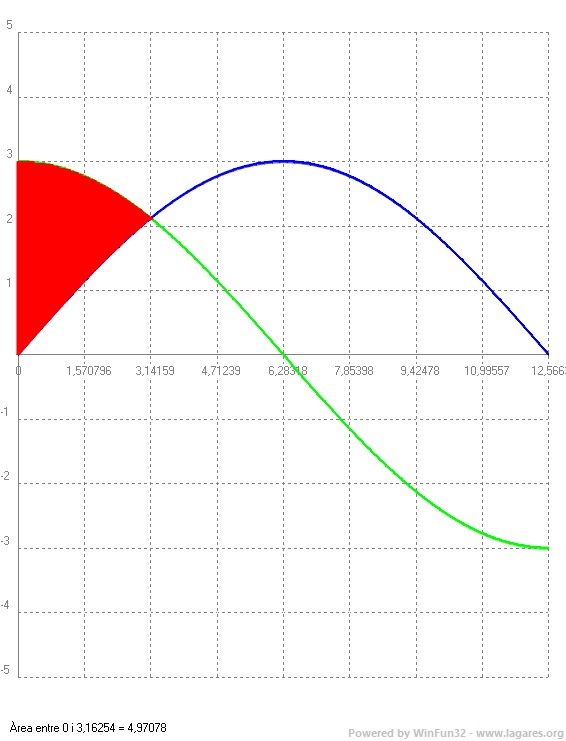 |