|
Funcions
Derivades
1. (2009-setembre-1) 3. Sigui f (x) = 2x3 – x2 + 3x + 1. Donades les rectes r1: y = x + 2 i r2: y = 7x – 2: a) Expliqueu, raonadament, si alguna de les dues rectes pot ser tangent a la corba y = f (x) en algun punt. b) En cas que alguna d’elles ho sigui, trobeu el punt de tangència. [1 punt per cada apartat] Solució amb el programa WinFun
2. (2009-setembre-1)
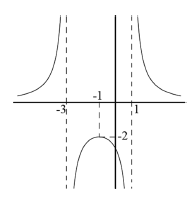
5. Considereu
la funció real de variable real a) Trobeu-ne el domini. b) Calculeu l’equació de les seves asímptotes, si en té. c) Estudieu-ne els intervals de creixement i de decreixement, així com les abscisses dels seus extrems relatius, si en té, i classifiqueu-los. [0,5 punts per l’apartat a; 1,5 punts per l’apartat b; 2 punts per l’apartat c]
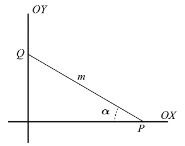
3. (2010-juny-1) 3. Un segment de longitud fixada m recolza sobre els eixos de coordenades. Calculeu el
valor de l’angle determinat pel segment amb els eixos i del qual m és la hipotenusa tingui àrea màxima. Comproveu que es tracta realment d’un màxim.
[2 punts] Solució amb trigonometria
4. (2010-juny-4) 3. Sigui P(x) = ax2+ bx + c un polinomi qualsevol de segon grau. a) Trobeu la relació existent entre els paràmetres a, b i c sabent que es compleix que P(1) = 0 i P(2) = 0. b) Quan es compleix la condició anterior, indiqueu quins valors pot tenir P'(3/2). [1 punt per cada apartat]
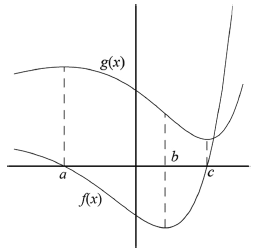
5. (2010-juny-4) 5. En la figura següent es representen dues funcions. L’una és la derivada de l’altra. Decidiu si la funció f (x) és la derivada de la funció g(x) o és a l’inrevés, estudiantquè passa en els punts x = a, x = b i x = c.
[2 punts]
6. (2010-juny-5)
3. Determineu
el valor dels paràmetres a, b i c perquè la gràfica de la funció
[2 punts]
7. (2010-setembre-2) 3. Considereu tots els prismes rectes de base quadrada amb un volum V fixat. Anomeneu x el costat de la base del prisma i y la seva altura. a) Trobeu l’expressió del volum i de l’àrea total del prisma en funció de les variables x i y. b) Comproveu que el que té àrea total mínima és en realitat un cub. [0,5 punts per l’apartat a; 1,5 punts per l’apartat b]
8. (2011-juny-1) 6. Sigui f (x)=x2 · e–ax quan a≠0. a) Calculeu el valor de a perquè aquesta funció tingui un extrem relatiu en el punt d’abscissa x=2. b) Quan a=2, classifiqueu-ne els extrems relatius. [1 punt per cada apartat]
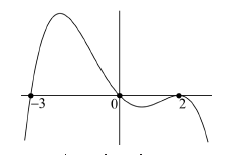
9. (2011-juny-4) 3. La gràfica corresponent a la derivada d’una funció f(x) és la següent:
a) Expliqueu raonadament quins valors de x corresponen a màxims o a mínims relatius de f(x). b) Determineu els intervals de creixement i decreixement de la funció f(x). [1,5 punts per l’apartat a; 0,5 punts per l’apartat b]
10. (2011-juny-4) 6. Dins d’un triangle rectangle, de catets 3 i 4 cm, hi ha un rectangle. Dos costats del rectangle estan situats en els catets del triangle i un dels vèrtexs del rectangle és a la hipotenusa del triangle. a) Feu un esbós de la situació descrita. b) Si x és la longitud del costat del rectangle que està situat en el catet petit i y és l’altre costat del rectangle, comproveu que es compleix que 4x+3y=12. c) Determineu les dimensions del rectangle perquè l’àrea sigui màxima. [0,5 punts per l’apartat a; 0,5 punts per l’apartat b; 1 punt per l’apartat c]
11. (2011-setembre-2) 3. Donada la funció f (x)=x3+ ax2+ bx+ c: a) Determineu la relació que han de complir els paràmetres a, b i c perquè f (x) tingui un extrem relatiu en el punt d’abscissa x = −1. b) Calculeu el valor del paràmetre a perquè hi hagi un punt d’inflexió de la funció f (x) en el punt d’abscissa x=0. c) Determineu la relació entre els paràmetres a, b i c sabent que la gràfica de f (x) talla l’eix OX en el punt d’abscissa x = −2. d) Calculeu el valor dels paràmetres a, b i c perquè es compleixin les tres propietats anteriors alhora.
|