|
(2009-setembre-1) 3. Sigui f (x) = 2x3 – x2 + 3x + 1. Donades les rectes r1: y = x + 2 i r2: y = 7x – 2: a) Expliqueu, raonadament, si alguna de les dues rectes pot ser tangent a la corba y = f (x) en algun punt. b) En cas que alguna d’elles ho sigui, trobeu el punt de tangència. [1 punt per cada apartat]
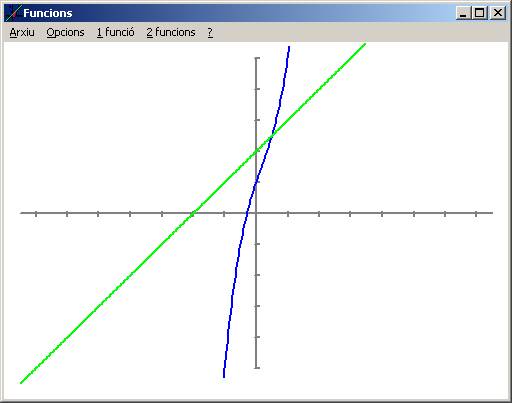
Origen Eix X: -7,5 Origen Eix Y: -5 Unitat Eix X: 1 Unitat Eix Y: 1 Final Eix X: 7,5 Final Eix Y: 5
F(x) = 2x^3-x^2+3x+1 G(x) = x+2
f(x) i r1 no són tangents en cap punt Origen Eix X: -7,5 Origen Eix Y: -15 Unitat Eix X: 1 Unitat Eix Y: 1 Final Eix X: 7,5 Final Eix Y: 10
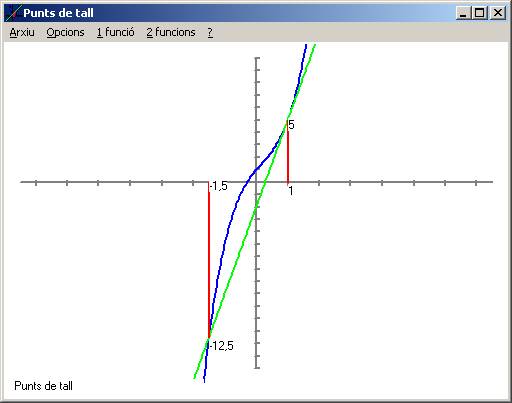
F(x) = 2x^3-x^2+3x+1 G(x) = 7x-2
Menú 2 Funcions – Punts de tall.
Origen Eix X: -7,5 Origen Eix Y: -15 Unitat Eix X: 1 Unitat Eix Y: 1 Final Eix X: 7,5 Final Eix Y: 10
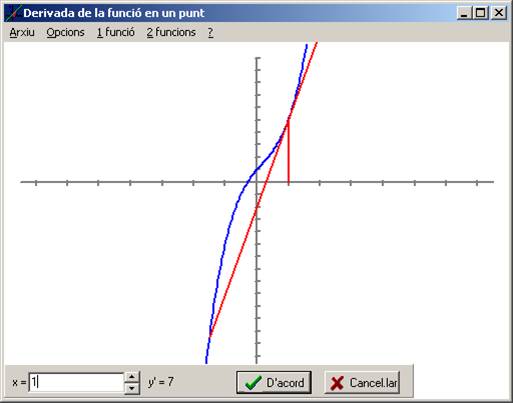
F(x) = 2x^3-x^2+3x+1
Menú 1 funció - Derivada de la funció en un punt en el punt 1
En el punt (1, 5) són tangents ja que f(x) i r2 passen per aquest punt i que la derivada de la f(x) val 7 en aquest punt i el pendent de la recta r2 val 7 |