|
L’examen consta de QUATRE exercicis obligatoris. Cada exercici val 2,5 punts. Feu els exerci-cis 1, 2 i 3 responent a TOTES les qüestions que s’hi plantegen. A l’exercici 4, trieu UNA de les dues opcions (A o B) proposades. En totes les respostes, expliqueu sempre què voleu fer i per què. Cal que la redacció de la resposta es faci de manera coherent, amb correcció i claredat, emprant la notació i el vocabulari matemàtic adequats i expressant la solució de manera clara. Podeu utilitzar les pàgines en blanc del final del quadern per a fer esquemes, esborranys, etc., o per a acabar de respondre a algun exercici si necessiteu més espai. En aquest últim cas, cal que ho indiqueu clarament al final de la pàgina de l’exercici corresponent. Podeu utilitzar calculadora, però no es permet l’ús de calculadores o altres aparells capaços d’emmagatzemar dades o de transmetre o rebre informació. 1-Considereu la funció `f(x)=(x^2-2x)/(x-1)`. a) Determineu els talls de la corba `y = f(x)` amb els eixos de coordenades, i les equacions de les seves possibles asímptotes verticals, horitzontals i obliqües. [1 punt] b) Calculeu les equacions de les rectes tangents a la corba `y = f(x)` en els punts `x = 0` i `x = 2`. Aquestes dues rectes són para?leles? Justifiqueu la resposta. [1 punt] c) Hi ha algun punt on la recta tangent a `f(x)` tingui pendent `1`? En cas afirmatiu, tro-beu-lo. [0,5 punts] SOLUCIÓ 2-Considereu el sistema d’equacions lineals següent: $$ \begin{cases} y-z=p+3\\ p^2x-z=5\\ x-y=3 \end{cases} $$ a) Discutiu el sistema per als diferents valors del paràmetre p. [1,25 punts] b) Resoleu el sistema per al cas `p = –1`. [0,5 punts] c) Per al cas `p = –1`, hi ha alguna solució que compleixi, a més, `xy = 10`? En cas afirmatiu, indiqueu quantes n’hi ha i trobeu-les totes. [0,75 punts] 3-Una empresa produeix dos tipus de peces, de ferro i d’acer. El `60 %` de la producció total correspon a peces de ferro i la resta són d’acer. Sabem que el `95 %` de les peces de ferro produïdes no tenen cap defecte, mentre que el `3 %` de les peces d’acer són defectuoses. a) Si agafem una peça a l’atzar, quina és la probabilitat que sigui defectuosa? [0,75 punts] b ) L’empresa aviat diversificarà la producció i començarà a produir també peces de titani, que es vendran en paquets de `5`. Si la probabilitat que una peça de titani sigui defectuosa és un valor desconegut `p`, i cada peça és defectuosa independentment de les altres, comproveu que l’expressió que ens dona la probabilitat que en un paquet de `5` peces n’hi hagi exactament `4` de defectuoses (en funció de `p`) és `f(p) = 5(p^4 – p^5)`. [0,75 punts] c) Considereu la funció `f(p)` de l’apartat anterior. Determineu el valor màxim que pren `f(p)` quan `p >= 0`. [1 punt] 4-Trieu UNA de les dues opcions (A o B) i responeu a les qüestions que s’hi plantegen. OPCIÓ A La vela major d’un veler té forma semiparabòlica i està delimitada per les gràfiques de `f(x) = –x^2 + 25`, `y = 0` i` x = 0`, tal com s’indica a la figura següent: 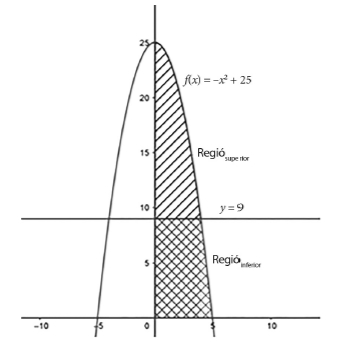 La vela té dues parts separades per la recta `y = 9`. Per a construir-la, s’empra un teixit de niló a la part superior, que costa `50` €/`u^2`, i un teixit de polièster a la part inferior, que costa `70` €/`u^2`. Calculeu el cost total del material que es necessita per a construir aquesta vela. [2,5 punts] SOLUCIÓ OPCIÓ B Considereu el pla p d’equació `x + y = 0`. a) Calculeu l’equació del pla `\pi'` que és perpendicular a `\pi` i conté els punts `P = (1, –1, 2)` i `Q = (3, –3, 6)`. [1 punt] b) Calculeu l’equació paramètrica de la recta continguda en `\pi'` i que conté els punts de `\pi'` a la mateixa distància de `P` que de `Q`. [1,5 punts] |