|
(2025-juny-1-4A)La vela major d’un veler té forma semiparabòlica i està delimitada per les gràfiques de `f(x) = –x^2 + 25`, `y = 0` i` x = 0`, tal com s’indica a la figura següent: 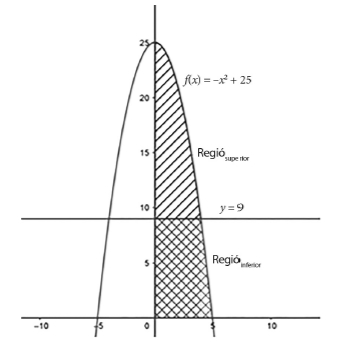 La vela té dues parts separades per la recta `y = 9`. Per a construir-la, s’empra un teixit de niló a la part superior, que costa `50` €/`u^2`, i un teixit de polièster a la part inferior, que costa `70` €/`u^2`. Calculeu el cost total del material que es necessita per a construir aquesta vela. [2,5 punts] Solució: Dividirem la regió en tres regions i calcularem de forma independent l'àrea en cadascula d'elles: 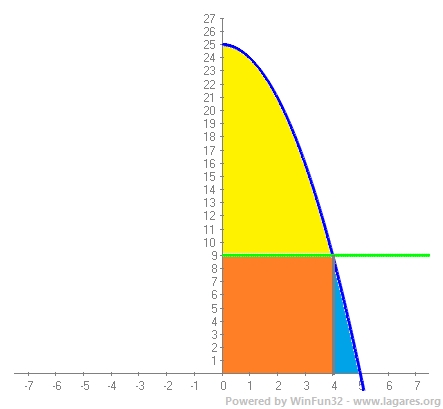 1-(Àrea groga) Cal calcular l'àrea que queda per sota la funció, `f(x) = –x^2 + 25` i per sobre la funció, `y = 9` i multiplicar-ho pel seu preu `50` €/`u^2`. Cal trobar el punt de tall, `x`, entre `f(x) = –x^2 + 25` i `y = 9`
`-x^2+25-9=0` `-x^2+16=0` `x^2=16 => x=\sqrt{16}=4` La solució negativa no interessa. Ara cal calcular: `\int_0^4 (f(x)-y) dx=\int_0^4 (-x^2+25-9) dx=\int_0^4 (-x^2+16) dx=[-x^3/3+16x]_0^4=(-4^3/3+16·4)-(-0^3/3+16·0)=-64/3+64=128/3 m^2` Que pel preu, `50` €/`u^2`, costa `128/3*50 = 2133,333` `€`. 2-Ara calcular el cost de la vela de sota.
Àrea `=9·4=36` `m^2` 2-2-(Àrea blau marí) Ara falta calcular l'àrea de l'últim tros de la paràbola que és la que queda sota, `f(x) = –x^2 + 25` per sobre de, `y=0` entre `x=4` i `x=5`. `\int_4^5 (–x^2 + 25) dx = [-x^3/3+25x]_4^5=(-5^3/3+25·5)-(-4^3/3+25·4)=-125/3+125+64/3-100=25-61/3=75/3-61/3=14/3` `m^2` Per calcular el cost de la segona regió cal sumar les dues àrees i multiplicar-les pel seu preu. Preu segona àrea `=(36+14/3)*70 = 2846,666` `€` Si sumen les dues quantitats tindrem el preu total `= 2133,333+2846,666 = 4980` `€` |