|
Què és el que se suposa que has de saber? No sols se suposa, ho has de saber fer entre moltes altres coses. -Resol,
-Resol,
-Resol,
-Extreu factor comú,
Si l'equació és completa, per resoldre-la, tenim la fórmula: `x=(-b \pm sqrt(b^2-4ac))/(2a)` -Resol, `x^2+4x-5=0` SOLUCIÓ:
`x=(-4 \pm sqrt(4^2-4·1·(-5)))/(2·1)=(-4 \pm sqrt(36))/2`
`x_2=(-4 - 6)/2=-5` -Resol, `x^2=4x` SOLUCIÓ:
`x(x-4)=0`
`x-4=0`
-Resol, `x^2-36=0` SOLUCIÓ:
`x^2=36` `x=sqrt(36)`
`x_2=-6` -Resol, `x^2+5=-4x` SOLUCIÓ:
`x^2+4x+5=0` `x=(-4 \pm sqrt(4^2-4·1·5))/(2·1)=(-4 \pm sqrt(16-20))/2=(-4 \pm sqrt(-4))/2` Com que surt una `sqrt(-)`, aquesta equació no té cap solució en els nombres reals. -Resol, `2x^2-4x=9` SOLUCIÓ:
`2x^2-4x-9=0` `x=(4 \pm sqrt((-4)^2-4·2·(-9)))/(2·2)=(-4 \pm sqrt(88))/4`
`x_2=(4 - sqrt(88))/4` Més endavant descobrirem que això es pot posar:
`x_2=1 - sqrt(11/2)`  -Calcula, `(x+3)^2` SOLUCIÓ:
-Calcula, `(2x+7)·(2x-7)` SOLUCIÓ:
-Calcula, `(3a-5)^2` SOLUCIÓ:
-Calcula, `(2a+3b)^2` SOLUCIÓ:
-Resol pels tres mètodes SOLUCIÓ:
$$ \begin{cases} x+2y = 8 \\ \\ 3x-y=3 \end{cases} $$ $$ \begin{cases} x+2y = 8 \\ \\ 2·(3x-y=3) \end{cases} $$ $$ \begin{cases} x+2y = 8 \\ \\ 6x-2y=6 \end{cases} $$ Sumen les dues equacions: `7x=14 => x=14/7 => x=2` Substituïm `x=2` a qualsevol de les dues equacions: `x+2y = 8 => 2+2y=8 => 2y=6 => y=3` $$ \begin{cases} x+2y = 8 \\ \\ 3x-y=3 \end{cases} $$ Aïllem una incògnita, per exemple `x`, a una equació, per exemple la primera: `x+2y = 8 => x=8-2y` El resultat el substituïm a la segona equació: `3x-y=3 => 3(8-2y)-y=3 => 24-6y-y=3 => -7y=-21 => y=3` Igualació: $$ \begin{cases} x+2y = 8 \\ \\ 3x-y=3 \end{cases} $$ Aïllem una incògnita, per exemple `x`, en la primera equació: `x+2y = 8 => x=8-2y` Aïllem la mateixa incògnita en la segona equació: `3x-y=3 => 3x=y+3 => x=(y+3)/3` Igualem les dues expresions. `8-2y=(y+3)/3` `3·(8-2y)=y+3` `24-6y=y+3` `24-3=y+6y` `21=7y` `y=21/7=3` El resultat el substituïm qualsevol de les dues expressions: `x=8-2y => x=8-2·3=2` -Calcula la mesura del costat que no es coneix. 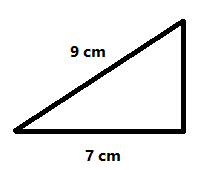 SOLUCIÓ:
`x^2+7^2=9^2` `x^2+49=81` `x^2=81-49` `x^2=32` `x=sqrt(32)` -Calcula l'àrea i el perímetre de la figura següent. 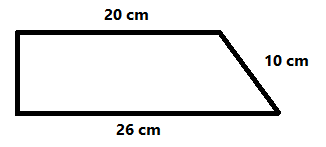 SOLUCIÓ: 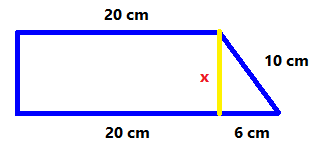
`x^2+6^2=10^2` `x^2+36=100` `x^2=100-36 = 64 => x=sqrt(64)=8`  Per al qual cosa el perímetre serà: Perímetre`=8+26+10+20=64 cm` I l'àrea caldrà calcular l'area del rectangle i sumar-li la del triangle: Àrea `= 20·8 + (6·8)/2= 160+24=184 cm^2` -Opera, `(x^3-4x^2-6x-3) + (2x^4-3x^3+2x^2+8)` SOLUCIÓ:
-Opera, `(x^3+5x^2-2x+4) - (-4x^4+3x^3+2x^2+7)` SOLUCIÓ:
-Opera, `(x^3-4x^2-6x-3) · (2x^2-x+3)` SOLUCIÓ:
-Calcula el valor numèric del polinomi, `2x^4-3x^3+2x^2+8` pel número `3`. SOLUCIÓ:
`P(x)=2x^4-3x^3+2x^2+8` `P(3)=2·3^4-3·3^3+2·3^2+8= 162-81+18+8=107` -Dibuixa la gràfica de les funcions següents: 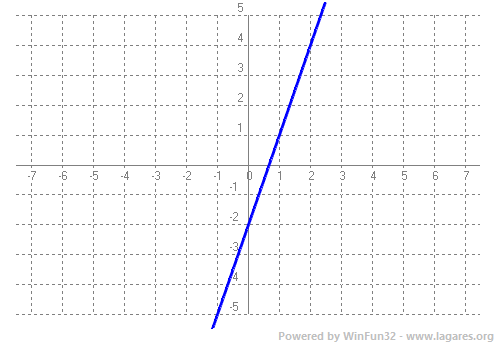 `g(x)=x^2-2x` 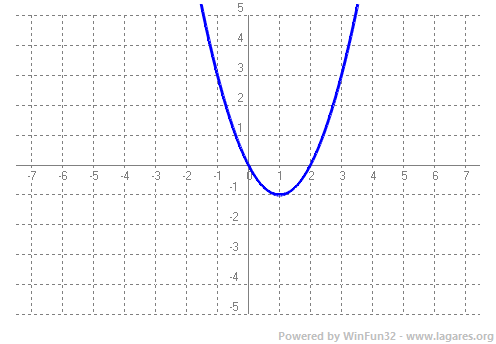 `y = 3` 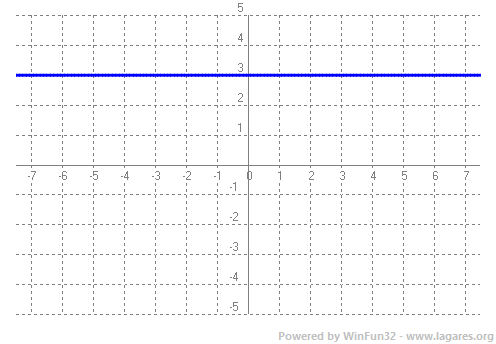 `x = -1` 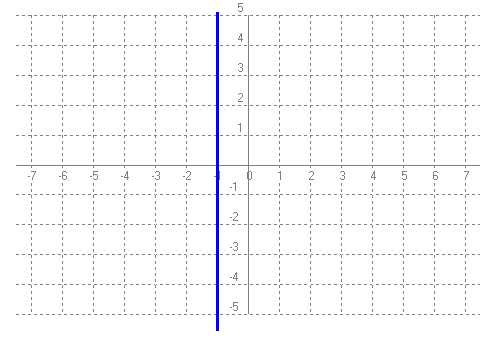 |