 Per si fos del teu interés et recomanem el següent article: REPTE INICIAL: 0) Quant mesura la distància a l'horitzó? Suposem estar damunt una muntanya que fa 1'124 kil˛metres d'altura i el radi de la Terra 6366'197 km. Índex:
b) Solució x2 + c = 0 c) Solució x2 + bx = 0 d) Exemples previs al cas general e) Solució ax2 + bx + c = 0. Fórmula general f) Exercicis per practicar Començarem per veure el cas b = 0: Veiem un altre exemple: El cas c = 0: Anem a veure el cas general: Per fer-ho comencem amb un exemple concret: Recorda: (a + b)2 = a2 + 2ab + b2 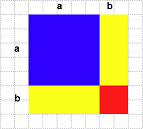 Hem vist la solució quan el polinomi és un quadrat perfecte. Com ho podem fer si no ho és? Anem a descobrir la fórmula per resoldre en general qualsevol equació de segon grau: Per ajudar a descobrir la fórmula en primer lloc veurem quan val el quadrat següent: I ara sí, aquí tens el perquè de la famosa fórmula per resoldre una equació de segon grau: Anem a veure com s'aplica en el cas anterior: Per practicar et proposem les següents equacions (i problemes) perquè els resolguis:
) x2 - 4 = 0 ) 2x2 - 18 = 0 ) -3x2 + 48 = 0 ) x2 - 5x = 0 ) x2 + 3x = 2x2 -5x ) x2 - 6x + 8 = 0 ) x2 + x + 1 = 0 ) x2 + 4x + 4 = 0 ) 3x2 + 9x + 6 = 0 ) 2x2 - 10x = -6 ) -3x2 = - 6x + 3 ) Tenim un triangle rectangle que el catet més gran mesura 1 dm més que el petit i l'hipotenusa 1 dm més que el catet gran. Quant mesura cada costat? ) El mateix problema anterior però suposant que la diferència entre costats és de 5 cm. ) Sabries resoldre el problema anterior suposant que la diferència entre el que mesura cada costat és una quantitat qualsevol. |