Receptes de física. Equació d'Schrödinger. Solució, àtoms amb un electró [H (hidrògen)] Llibre Física Cuántica (Eisberg, Resnick) 1-Ingredients 1-Equació d'Schrödinger. `-ℏ^2/(2m)(\delta^2 \Psi(\vec(x),t))/(\delta \vec(x)^2)+V(\vec(x),t)\Psi(\vec(x),t)=iℏ(\delta \Psi(\vec(x),t))/(\delta t)` 2-`\mu` massa reduïda. `\mu=((M)/(m+M))·m` 3-Potencial elèctric produït pel nucli amb `Z` protons. `V(x,y,z)=(-Ze^2)/(4\pi\epsilon_0 sqrt(x^2+y^2+z^2))` 4-Potencial elèctric produït pel nucli amb `Z` protons en coordenades polars. Recordem `sqrt(x^2+y^2+z^2)=r` `V(r)=(-Ze^2)/(4\pi\epsilon_0 r)` 5-Separació de la funció d'ona en la part espaial i temporal pels potencials que no depenen del temps. `\Psi(x,y,z,t)=\psi(x,y,z)e^(-i(ET)/ℏ)` 6-Operador Laplacià en coordenades rectangulars. `\nabla^2=\delta^2/(\deltax^2)+\delta^2/(\deltay^2)+\delta^2/(\deltaz^2)` 7-Operador Laplaciá en coordenades polars. `\nabla^2=1/r^2\delta/(\deltar)(r^2\delta/(\deltar))+1/(r^2sin^2\theta)\delta^2/(\delta\varphi^2)+1/(r^2sin\theta)\delta/(\delta\theta)(sin\theta\delta/(\delta\theta))` (1-7) 2-Càlculs 1-Equació d'Schrödinger en coordenades rectangulars. `-ℏ^2/(2\mu)[(\delta^2 \Psi(x,y,z,t))/(\delta x^2)+(\delta^2 \Psi(x,y,z,t))/(\delta y^2)+(\delta^2 \Psi(x,y,z,t))/(\delta z^2)]+V(x,y,z,t)\Psi(x,y,z,t)=iℏ(\delta \Psi(x,y,z,t))/(\delta t)` 2-Equació d'Schrödinger en coordenades rectangulars simplificada. `-ℏ^2/(2\mu)\nabla^2\Psi+ V\Psi = i ℏ (\delta\Psi)/(\deltat)` 3-Si `V(x,y,z,t)` no depèn de `t`, que no és el cas, ja que `V(x,y,z)=(-Ze^2)/(4\pi\epsilon_0 r)` `=>` `-ℏ^2/(2\mu)\nabla^2\psi(x,y,z)e^(-i(ET)/ℏ)+ V(x,y,z)\psi(x,y,z)e^(-i(ET)/ℏ) = i ℏ (\delta\psi(x,y,z)e^(-i(ET)/ℏ))/(\deltat)` `-ℏ^2/(2\mu)\nabla^2\psi(x,y,z)e^(-i(ET)/ℏ)+ V(x,y,z)\psi(x,y,z)e^(-i(ET)/ℏ) = i ℏ (\psi(x,y,z)e^(-i(ET)/ℏ))(-iE/ℏ)` `-ℏ^2/(2\mu)\nabla^2\psi(x,y,z)e^(-i(ET)/ℏ)+ V(x,y,z)\psi(x,y,z)·e^(-i(ET)/ℏ) = i·ℏ·(-i)·E/ℏ·\psi(x,y,z)·e^(-i(ET)/ℏ)` `-ℏ^2/(2\mu)\nabla^2\psi(x,y,z)+ V(x,y,z)\psi(x,y,z) = E\psi(x,y,z)` (2-3) 4-Si expressem, `\psi(x,y,z)` en coordenades polars, `\psi(r,\theta,\varphi)` i expressant el Laplacià en coordenades polars es poden trobar solucions a l'equació d'Schrödinger de la forma (ressolució de l'equació diferencial per separació de variables): `\psi(x,y,z)=R(r)·\Theta(\theta)·\Phi(\varphi)` (2-4) 5-Posant (1-7) i (2-4) a (2-3). `-ℏ^2/(2\mu)[1/r^2\delta/(\deltar)(r^2(\deltaR(r)·\Theta(\theta)·\Phi(\varphi))/(\deltar))+1/(r^2sin^2\theta)(\delta^2R(r)·\Theta(\theta)·\Phi(\varphi))/(\delta\varphi^2)+1/(r^2sin\theta)\delta/(\delta\theta)(sin\theta(\deltaR(r)·\Theta(\theta)·\Phi(\varphi))/(\delta\theta))]+V(r)R(r)·\Theta(\theta)·\Phi(\varphi)=E·R(r)·\Theta(\theta)·\Phi(\varphi)` 6-Escrivint-la un xic més simplificada, sense les variablesm independents de les diferents funcions. `-ℏ^2/(2\mu)[1/r^2\delta/(\deltar)(r^2(\deltaR·\Theta·\Phi)/(\deltar))+1/(r^2sin^2\theta)(\delta^2R·\Theta·\Phi)/(\delta\varphi^2)+1/(r^2sin\theta)\delta/(\delta\theta)(sin\theta(\deltaR·\Theta·\Phi)/(\delta\theta))]+V(r)·R·\Theta·\Phi=E·R·\Theta·\Phi` 7-Com les derivades parcials són un producte de funcions, amb variables separades, podem treure les funcions que no tenen la variable que derivem a fora multiplicant i les derivades parcials es converteixen en derivades normals ja que les funcions que derivem només tenen la variable que derivem. `-ℏ^2/(2\mu)[(\Theta·\Phi)/r^2 d/(dr)(r^2(dR)/(dr))+(R·\Theta)/(r^2sin^2\theta)(d^2\Phi)/(d\varphi^2)+(R·\Phi)/(r^2sin\theta)d/(d\theta)(sin\theta(d\Theta)/(d\theta))]+V(r)·R·\Theta·\Phi=E·R·\Theta·\Phi` 8-Ho multipliquem tot per `(-2\mu·r^2·sin^2\theta)/(R·\Theta·\Phi·h^2)` `(sin^2\theta)/R d/(dr)(r^2(dR)/(dr))+1/\Phi(d^2\Phi)/(d\varphi^2)+(sin\theta)/(\Theta)d/(d\theta)(sin\theta(d\Theta)/(d\theta)) + (-2\mu·r^2·sin^2\theta)/ℏ^2 · V(r)=(-2\mu·r^2·sin^2\theta)/ℏ^2 ·E` 9-Passem a l'esquerra tot menys el segon sumand i amb el terme amb `V` i `E` treiem factor comú, `-2\mu/ℏ^2·r^2·sin^2\theta`. `1/\Phi(d^2\Phi)/(d\varphi^2) = -(sin^2\theta)/R d/(dr)(r^2(dR)/(dr)) -(sin\theta)/(\Theta)d/(d\theta)(sin\theta(d\Theta)/(d\theta))-(2\mu)/ℏ^2·r^2·sin^2\theta[E-V(r)]` 10-Com el primer membre de la igualtat no depèn ni de `r` ni de `\theta` i el segon no depèn de `\phi`, el resultat de cada costat no pot deprendre de cap d'aquestes variables. Ho sigui el valor comú ha de ser una constant i, per conveniència en direm `-m_l^2`. Si ho igualem a cada costat. a) `1/\Phi(d^2\Phi)/(d\varphi^2)=-m_l^2 => (d^2\Phi)/(d\varphi^2)=-m_l^2· \Phi` b) `-(sin^2\theta)/R d/(dr)(r^2(dR)/(dr)) -(sin\theta)/(\Theta)d/(d\theta)(sin\theta(d\Theta)/(d\theta))-(2\mu)/ℏ^2·r^2·sin^2\theta[E-V(r)]=-m_l^2` O dividim tot per `sin^2\theta`. `-1/R d/(dr)(r^2(dR)/(dr)) -1/(\Theta·sin\theta)d/(d\theta)(sin\theta(d\Theta)/(d\theta))-(2\mu)/ℏ^2·r^2[E-V(r)]=-m_l^2/(sin^2\theta)` Canviem tot de signe i passem el segon sumand a la dreta. `1/R d/(dr)(r^2(dR)/(dr)) + (2\mu·r^2)/ℏ^2[E-V(r)]=-1/(\Theta·sin\theta)d/(d\theta)(sin\theta(d\Theta)/(d\theta))+m_l^2/(sin^2\theta)` 11-Igual que abans tornem a tenir una igualtat on tenim separades les variables, per la qual cosa cadascuna d'elles serà igual a una constant que per conveniència n'hi direm, `l(l+1)`. a) `-1/(\Theta·sin\theta)d/(d\theta)(sin\theta(d\Theta)/(d\theta))+m_l^2/(sin^2\theta)=l(l+1)` b) `1/R d/(dr)(r^2(dR)/(dr)) + (2\mu·r^2)/ℏ^2[E-V(r)]=l(l+1)` Ho multipliquem tot per `R/r` `1/r^2 d/(dr)(r^2(dR)/(dr)) + (2\mu)/ℏ^2[E-V(r)]·R=l(l+1)R/r^2` 12-Resum, hem aconseguit tres equacions diferencials amb les variables separades: i- `(d^2\Phi)/(d\varphi^2)=-m_l^2· \Phi` ii- `-1/(\Theta·sin\theta)d/(d\theta)(sin\theta(d\Theta)/(d\theta))+m_l^2/(sin^2\theta)=l(l+1)` iii- `1/r^2 d/(dr)(r^2(dR)/(dr)) + (2\mu)/ℏ^2[E-V(r)]·R=l(l+1)R/r^2` 13- Solució de la primera. `(d^2\Phi(\varphi))/(d\varphi^2)=-m_l^2· \Phi(\varphi)` `\Phi(\varphi)=e^(im_l\varphi)` Com que la funció ha de ser univaluada `=> \Phi(o)=\Phi(2\pi)` `e^(im_l 0)=e^(im_1 2\pi)` `1=cos(m_l 2\pi) + i sin(m_l 2\pi)` Això implica que el valor de `m_l` només pot ser un nombre enter: `m_l=... -3, -2, -1, 0, 1, 2, 3, ...` SOLUCIÓ: `(d^2\Phi(\varphi))/(d\varphi^2)=-m_l^2· \Phi(\varphi)` `e^(im_l 0)=e^(im_1 2\pi)` amb `m_l=... -3, -2, -1, 0, 1, 2, 3, ...` 14- Solució de la segona. Demostració per més endavant `-1/(\Theta·sin\theta)d/(d\theta)(sin\theta(d\Theta)/(d\theta))+m_l^2/(sin^2\theta)=l(l+1)` SOLUCIÓ: `l= |m_l|, |m_l|+1, |m_l|+2, ...` `\Theta_(lm_l) (\theta)=sin^(|m_l|)(\theta) · F_(lm_l) (cos(\theta))` On `F_(lm_l) (cos(\theta))` són polinomis en `cos(\theta)`. 15- Solució de la tercera. Demostració per més endavant `1/r^2 d/(dr)(r^2(dR)/(dr)) + (2\mu)/ℏ^2[E-V(r)]·R=l(l+1)R/r^2` SOLUCIÓ: `E_n=-(\MZ^2e^4)/((4\pi\epsilon_0)^2 2ℏ^2n^2`. `n = l+1, l+2, l+3, ...` `R_(nl) (r) = e^(-(Zr)/(na_0)) ((Zr)/a_0)^l G_(nl) ((Zr)/a_0)` `a_0=(4\pi\epsilon_0 ℏ^2)/(\mue^2)` Per dibuixar les gràfiques fem servir que la unitat atòmica val `a_0=1`. Radi de Bohr. `R_(1,0)(r)=2/a_o^(3/2)e^(-r/a_0)` 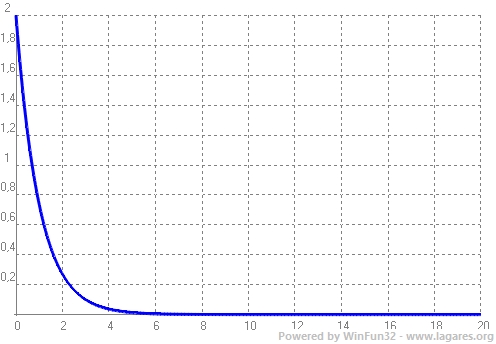2*exp(-x) `R_(2,0)(r)=1/(2\sqrt{2}·a_o^(3/2))[-r/a_0+2]·e^(-r/(2a_0)` `R_(2,1)(r)=1/(2\sqrt{2}·a_o^(3/2))·r/a_0·e^(-r/(2a_0)` 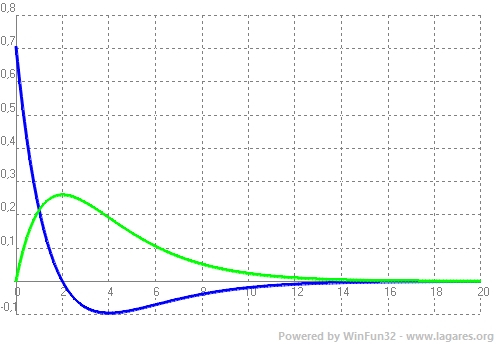1/(2*2^0,5)*(2-x)*exp(-x/2) 1/(2*2^0,5)*x*exp(-x/2) `R_(3,0)(r)=2/(81\sqrt{3}·a_0^(3/2))·[2*(r/a_0)^2-18·r/a_0+27]·e^(-r/(3a_0))` `R_(3,1)(r)=4/(81\sqrt{6}·a_0^(3/2))·[-(r/a_0)^2+6·r/a_0]·e^(-r/(3a_0))` `R_(3,2)(r)=4/(81\sqrt{30}·a_0^(3/2))·(r/a_0)^2·e^(-r/(3a_0))` 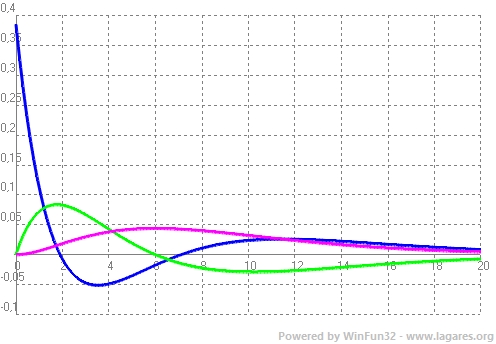2/(81*3^0,5)*(2x^2-18x+27)*exp(-x/3) 4/(81*6^0,5)*(6-x)*x*exp(-x/3) 4/(81*30^0,5)*x^2*exp(-x/3) Totes les funcions anteriors en una mateixa gràficara amb el mateix color per cada nivell: 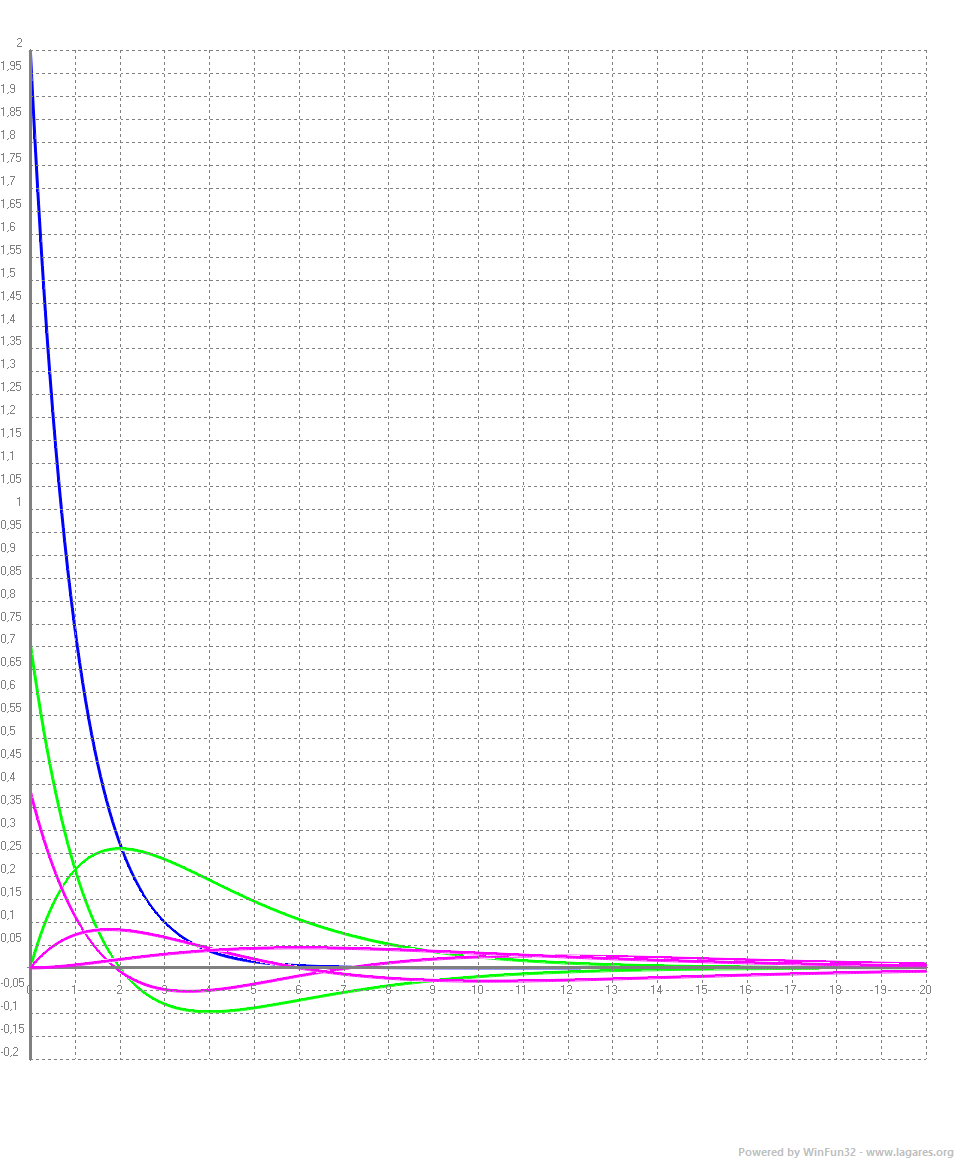Link externs interessants: El átomo de hidrógeno