|
1-Ingredients
2-Coordenades rectangulars en coordenades polars. `y=rsin\theta\sin\varphi` `z=rcos\theta` 3-Coordenades polars en coordenades rectangulars. `\theta=arc cos(z/sqrt(x^2+y^2+z^2))` `\varphi= arc tan (y/x)` 4-RESULTAT: Operador Laplaciá en coordenades polars. Si el que necessiteu és la fórmula, ja ho podeu deixar aquí. Si us va la marxa us convidem a continuar. Cal saber calcular derivades senzilles `1/x, sinx, cosx`, derivada del producte, derivada de la funció composta, ..., i relacions trigonomètriques senzilles (i importants) com `sin^2x+cos^2x=1`. Operacions amb matrius, càlcul de la matriu inversa, resolució de sistemes mitjançant matrius. Si ho desenvolupem: 1'-Càlcul operador Laplacià en coordenades polars 2D
2-Càlculs. 1a derivada `(\delta)/(\delta x)=(\delta)/(\delta r)(\delta r)/(\delta x)+(\delta)/(\delta\theta)(\delta\theta)/(\deltax)+(\delta)/(\delta\varphi)(\delta\varphi)/(\deltax)` `(\delta)/(\delta y)=(\delta)/(\delta r)(\delta r)/(\delta y)+(\delta)/(\delta\theta)(\delta\theta)/(\deltay)+(\delta)/(\delta\varphi)(\delta\varphi)/(\deltay)` `(\delta)/(\delta z)=(\delta)/(\delta r)(\delta r)/(\delta z)+(\delta)/(\delta\theta)(\delta\theta)/(\deltaz)+(\delta)/(\delta\varphi)(\delta\varphi)/(\deltaz)`
`(\delta)/(\deltar) = (\deltax)/(\deltar)(\delta)/(\deltax)+(\deltay)/(\deltar)(\delta)/(\deltay)+(\deltaz)/(\deltar)(\delta)/(\deltaz) = sin \theta cos \varphi(\delta)/(\deltax)+sin\theta\sin\varphi(\delta)/(\deltay)+cos\theta(\delta)/(\deltaz)` `(\delta)/(\delta\theta) = (\deltax)/(\delta\theta)(\delta)/(\deltax)+(\deltay)/(\delta\theta)(\delta)/(\deltay)+(\deltaz)/(\delta\theta)(\delta)/(\deltaz) = rcos \theta cos \varphi(\delta)/(\deltax)+rcos\theta\sin\varphi(\delta)/(\deltay)-rsin\theta(\delta)/(\deltaz)` `(\delta)/(\delta\varphi) = (\deltax)/(\delta\varphi)(\delta)/(\deltax)+(\deltay)/(\delta\varphi)(\delta)/(\deltay)+(\deltaz)/(\delta\varphi)(\delta)/(\deltaz) = -rsin \theta sin \varphi (\delta)/(\deltax)+rsin\theta\cos\varphi(\delta)/(\deltay)` Això ho podem veure com un sistema de 3 equacions amb 3 incògnites, `(\delta)/(\deltax)`, `(\delta)/(\deltay)`, `(\delta)/(\deltaz)`. Ho posem en notació matricial. $$ \begin{pmatrix} \frac{\delta}{\delta r}\\\ \frac{\delta}{\delta\theta}\\\ \frac{\delta}{\delta\varphi}\end{pmatrix}= \begin{pmatrix} sin \theta cos \varphi & sin\theta\sin\varphi & cos\theta\\\ rcos \theta cos \varphi & rcos \theta sin \varphi & -rsin\theta\\\ -rsin \theta sin \varphi & rsin\theta\cos\varphi & 0\end{pmatrix} · \begin{pmatrix} \frac{\delta}{\delta x}\\\ \frac{\delta}{\delta y}\\\ \frac{\delta}{\delta z}\end{pmatrix} $$ Ho girem per posar-ho de la forma tradicional, termes independents a la dreta. $$ \begin{pmatrix} sin \theta cos \varphi & sin\theta\sin\varphi & cos\theta\\\ rcos \theta cos \varphi & rcos \theta sin \varphi & -rsin\theta\\\ -rsin \theta sin \varphi & rsin\theta\cos\varphi & 0\end{pmatrix} · \begin{pmatrix} \frac{\delta}{\delta x}\\\ \frac{\delta}{\delta y}\\\ \frac{\delta}{\delta z}\end{pmatrix}= \begin{pmatrix} \frac{\delta}{\delta r}\\\ \frac{\delta}{\delta\theta}\\\ \frac{\delta}{\delta\varphi}\end{pmatrix} $$ Calculem la matriu inversa de la matriu del sistema i ho multipliquem per l'esquerra. $$ M · \begin{pmatrix} \frac{\delta}{\delta x}\\\ \frac{\delta}{\delta y}\\\ \frac{\delta}{\delta z}\end{pmatrix}= \begin{pmatrix} \frac{\delta}{\delta r}\\\ \frac{\delta}{\delta\theta}\\\ \frac{\delta}{\delta\varphi}\end{pmatrix} $$ $$ \begin{pmatrix} \frac{\delta}{\delta x}\\\ \frac{\delta}{\delta y}\\\ \frac{\delta}{\delta z}\end{pmatrix}= M^{-1} · \begin{pmatrix} \frac{\delta}{\delta r}\\\ \frac{\delta}{\delta\theta}\\\ \frac{\delta}{\delta\varphi}\end{pmatrix} $$ Per calcular `M^(-1)` en primer lloc calculem `det(M)` $$ \begin{vmatrix} sin \theta cos \varphi & sin\theta\sin\varphi & cos\theta\\\ rcos \theta cos \varphi & rcos \theta sin \varphi & -rsin\theta\\\ -rsin \theta sin \varphi & rsin\theta\cos\varphi & 0\end{vmatrix}= $$ Calculem la matriu d'adjunts `M^\star` $$ M=\begin{vmatrix} sin \theta cos \varphi & sin\theta\sin\varphi & cos\theta\\\ rcos \theta cos \varphi & rcos \theta sin \varphi & -rsin\theta\\\ -rsin \theta sin \varphi & rsin\theta\cos\varphi & 0\end{vmatrix} $$ $$ M^\star=\begin{pmatrix} \begin{vmatrix} rcos \theta sin \varphi & -rsin\theta\\\ rsin\theta\cos\varphi & 0\ \end{vmatrix}& -\begin{vmatrix} rcos \theta cos \varphi & -rsin\theta\\\ -rsin \theta sin \varphi & 0\end{vmatrix} & \begin{vmatrix} rcos \theta cos \varphi & rcos \theta sin \varphi\\\ -rsin \theta sin \varphi & rsin\theta\cos\varphi \end{vmatrix}\\\ -\begin{vmatrix} sin\theta\sin\varphi & cos\theta\\\ rsin\theta\cos\varphi & 0\end{vmatrix} & \begin{vmatrix}sin \theta cos \varphi & cos\theta\\\ -rsin \theta sin \varphi & 0 \end{vmatrix} & -\begin{vmatrix}sin \theta cos \varphi & sin\theta\sin\varphi\\\ -rsin \theta sin \varphi & rsin\theta\cos\varphi \end{vmatrix}\\\ \begin{vmatrix} sin\theta\sin\varphi & cos\theta\\\ rcos \theta sin \varphi & -rsin\theta\end{vmatrix} & -\begin{vmatrix} sin \theta cos \varphi & cos\theta\\\ rcos \theta cos \varphi & -rsin\theta\end{vmatrix} & \begin{vmatrix} sin \theta cos \varphi & sin\theta\sin\varphi\\\ rcos \theta cos \varphi & rcos \theta sin \varphi \end{vmatrix}\end{pmatrix} $$ $$ M^\star=\begin{pmatrix} r^2sin^2\theta\cos\varphi & r^2sin^2\theta\sin\varphi & r^2cos\theta sin\theta cos^2 \varphi + r^2cos \theta sin\theta sin^2 \varphi\\\ rsin\theta\cos\theta\cos\varphi & rsin\theta\cos\theta\sin\varphi & -rsin^2\theta\cos^2\varphi-rsin^2\theta\sin^2\varphi\\\ -rsin^2\theta sin\varphi -rcos^2\theta sin\varphi & rsin^2\theta cos\varphi +rcos^2\theta cos\varphi & rsin\theta cos\theta cos\varphi sin\varphi - rcos\theta sin\theta cos\varphi sin\varphi \end{pmatrix} $$ $$ M^\star=\begin{pmatrix} r^2sin^2\theta\cos\varphi & r^2sin^2\theta\sin\varphi & r^2cos \theta sin\theta\\\ rsin\theta\cos\theta\cos\varphi & rsin\theta\cos\theta\sin\varphi & -rsin^2\theta\\\ -rsin\varphi & rcos\varphi & 0 \end{pmatrix} $$ Calculem la matriu transposta `(M^\star)^t` $$ (M^\star)^t=\begin{pmatrix} r^2sin^2\theta\cos\varphi & rsin\theta\cos\theta\cos\varphi & -rsin\varphi\\\ r^2sin^2\theta\sin\varphi & rsin\theta\cos\theta\sin\varphi & rcos\varphi\\\ r^2cos \theta sin\theta & -rsin^2\theta & 0 \end{pmatrix} $$ Finalment per trobar la inversa cal dividir pel determinant `M^(-1)=(M^\star)^t/(det M)` $$ M^{-1}=\begin{pmatrix} \frac{r^2sin^2\theta\cos\varphi}{r^2sin\theta} & \frac{rsin\theta\cos\theta\cos\varphi}{r^2sin\theta} & \frac{-rsin\varphi}{r^2sin\theta} \\\ \frac{r^2sin^2\theta\sin\varphi}{r^2sin\theta} & \frac{rsin\theta\cos\theta\sin\varphi}{r^2sin\theta} & \frac{rcos\varphi}{r^2sin\theta} \\\ \frac{r^2cos \theta sin\theta}{r^2sin\theta} & \frac{-rsin^2\theta}{r^2sin\theta} & 0 \end{pmatrix} $$ $$ M^{-1}=\begin{pmatrix} sin\theta\cos\varphi & \frac{\cos\theta\cos\varphi}{r} & \frac{-sin\varphi}{rsin\theta} \\\ sin\theta\sin\varphi & \frac{\cos\theta\sin\varphi}{r} & \frac{cos\varphi}{rsin\theta} \\\ cos \theta & \frac{-sin\theta}{r} & 0 \end{pmatrix} $$ Finalment $$ \begin{pmatrix} \frac{\delta}{\delta x}\\\ \frac{\delta}{\delta y}\\\ \frac{\delta}{\delta z}\end{pmatrix}= M^{-1} · \begin{pmatrix} \frac{\delta}{\delta r}\\\ \frac{\delta}{\delta\theta}\\\ \frac{\delta}{\delta\varphi}\end{pmatrix} $$ $$ \begin{pmatrix} \frac{\delta}{\delta x}\\\ \frac{\delta}{\delta y}\\\ \frac{\delta}{\delta z}\end{pmatrix}= \begin{pmatrix} sin\theta\cos\varphi & \frac{\cos\theta\cos\varphi}{r} & \frac{-sin\varphi}{rsin\theta} \\\ sin\theta\sin\varphi & \frac{\cos\theta\sin\varphi}{r} & \frac{cos\varphi}{rsin\theta} \\\ cos \theta & \frac{-sin\theta}{r} & 0 \end{pmatrix} · \begin{pmatrix} \frac{\delta}{\delta r}\\\ \frac{\delta}{\delta\theta}\\\ \frac{\delta}{\delta\varphi}\end{pmatrix} $$ $$ \begin{pmatrix} \frac{\delta}{\delta x}\\\ \frac{\delta}{\delta y}\\\ \frac{\delta}{\delta z}\end{pmatrix}= \begin{pmatrix} sin\theta\cos\varphi\frac{\delta}{\delta r} & \frac{\cos\theta\cos\varphi}{r}\frac{\delta}{\delta\theta} & \frac{-sin\varphi}{rsin\theta}\frac{\delta}{\delta\varphi} \\\ sin\theta\sin\varphi\frac{\delta}{\delta r} & \frac{\cos\theta\sin\varphi}{r}\frac{\delta}{\delta\theta} & \frac{cos\varphi}{rsin\theta}\frac{\delta}{\delta\varphi} \\\ cos \theta\frac{\delta}{\delta r} & \frac{-sin\theta}{r}\frac{\delta}{\delta\theta} & 0 \end{pmatrix} · $$ En definitiva: $$ \frac{\delta}{\delta x}=sin\theta\cos\varphi\frac{\delta}{\delta r} + \frac{\cos\theta\cos\varphi}{r}\frac{\delta}{\delta\theta} + \frac{-sin\varphi}{rsin\theta}\frac{\delta}{\delta\varphi} $$ $$ \frac{\delta}{\delta y}=sin\theta\sin\varphi\frac{\delta}{\delta r} + \frac{\cos\theta\sin\varphi}{r}\frac{\delta}{\delta\theta} + \frac{cos\varphi}{rsin\theta}\frac{\delta}{\delta\varphi} $$ $$ \frac{\delta}{\delta z}=cos \theta\frac{\delta}{\delta r} + \frac{-sin\theta}{r}\frac{\delta}{\delta\theta} $$ 3-Càlculs. 2a derivada `\delta/(\deltax)(\delta/(\deltax))+\delta/(\deltay)(\delta/(\deltay))+\delta/(\deltaz)(\delta/(\deltaz))=` `\delta/(\deltax)(sin\thetacos\varphi\delta/(\deltar)+(cos\thetacos\varphi)/r\delta/(\delta\theta)-sin\varphi/(rsin\theta)\delta/(\delta\varphi))+` `\delta/(\deltay)(sin\thetasin\varphi\delta/(\deltar)+(cos\thetasin\varphi)/r\delta/(\delta\theta)+cos\varphi/(rsin\theta)\delta/(\delta\varphi))+` `\delta/(\deltaz)(cos\theta\delta/(\deltar)-sin\theta/r\delta/(\delta\theta))=` `(sin\thetacos\varphi\delta/(\deltar)+(cos\thetacos\varphi)/r\delta/(\delta\theta)-sin\varphi/(rsin\theta)\delta/(\delta\varphi))(sin\thetacos\varphi\delta/(\deltar)+(cos\thetacos\varphi)/r\delta/(\delta\theta)-sin\varphi/(rsin\theta)\delta/(\delta\varphi))+` `(sin\thetasin\varphi\delta/(\deltar)+(cos\thetasin\varphi)/r\delta/(\delta\theta)+cos\varphi/(rsin\theta)\delta/(\delta\varphi))(sin\thetasin\varphi\delta/(\deltar)+(cos\thetasin\varphi)/r\delta/(\delta\theta)+cos\varphi/(rsin\theta)\delta/(\delta\varphi))+` `(cos\theta\delta/(\deltar)-sin\theta/r\delta/(\delta\theta))(cos\theta\delta/(\deltar)-sin\theta/r\delta/(\delta\theta))=` `(sin\thetacos\varphi\delta/(\deltar))(sin\thetacos\varphi\delta/(\deltar)) + (sin\thetacos\varphi\delta/(\deltar))((cos\thetacos\varphi)/r\delta/(\delta\theta)) - (sin\thetacos\varphi\delta/(\deltar))(sin\varphi/(rsin\theta)\delta/(\delta\varphi))+` `((cos\thetacos\varphi)/r\delta/(\delta\theta))(sin\thetacos\varphi\delta/(\deltar)) + ((cos\thetacos\varphi)/r\delta/(\delta\theta))((cos\thetacos\varphi)/r\delta/(\delta\theta)) - ((cos\thetacos\varphi)/r\delta/(\delta\theta))(sin\varphi/(rsin\theta)\delta/(\delta\varphi))+` `(-sin\varphi/(rsin\theta)\delta/(\delta\varphi))(sin\thetacos\varphi\delta/(\deltar)) + (-sin\varphi/(rsin\theta)\delta/(\delta\varphi))((cos\thetacos\varphi)/r\delta/(\delta\theta)) - (-sin\varphi/(rsin\theta)\delta/(\delta\varphi))(sin\varphi/(rsin\theta)\delta/(\delta\varphi))+` `(sin\thetasin\varphi\delta/(\deltar))(sin\thetasin\varphi\delta/(\deltar))+(sin\thetasin\varphi\delta/(\deltar))((cos\thetasin\varphi)/r\delta/(\delta\theta))+(sin\thetasin\varphi\delta/(\deltar))(cos\varphi/(rsin\theta)\delta/(\delta\varphi))+` `((cos\thetasin\varphi)/r\delta/(\delta\theta))(sin\thetasin\varphi\delta/(\deltar))+((cos\thetasin\varphi)/r\delta/(\delta\theta))((cos\thetasin\varphi)/r\delta/(\delta\theta))+((cos\thetasin\varphi)/r\delta/(\delta\theta))(cos\varphi/(rsin\theta)\delta/(\delta\varphi))+` `(cos\varphi/(rsin\theta)\delta/(\delta\varphi))(sin\thetasin\varphi\delta/(\deltar))+(cos\varphi/(rsin\theta)\delta/(\delta\varphi))((cos\thetasin\varphi)/r\delta/(\delta\theta))+(cos\varphi/(rsin\theta)\delta/(\delta\varphi))(cos\varphi/(rsin\theta)\delta/(\delta\varphi))+` `(cos\theta\delta/(\deltar))(cos\theta\delta/(\deltar))-(cos\theta\delta/(\deltar))(sin\theta/r\delta/(\delta\theta))+` `-(sin\theta/r\delta/(\delta\theta))(cos\theta\delta/(\deltar))+(sin\theta/r\delta/(\delta\theta))(sin\theta/r\delta/(\delta\theta))=` `sin^2\thetacos^2\varphi\delta^2/(\deltar^2)-(sin\thetacos\thetacos^2\varphi)/r^2\delta/(\delta\theta)+(sin\thetacos\thetacos^2\varphi)/r\delta^2/(\deltar\delta\theta)+(cos\varphisin\varphi)/r^2\delta/(\delta\varphi)-(cos\varphisin\varphi)/r\delta^2/(\deltar\delta\varphi)+` `(cos^2\thetacos^2\varphi)/r\delta/(\deltar)+(cos\thetasin\thetacos^2\varphi)/r\delta^2/(\delta\theta\deltar)-(cos\thetasin\thetacos^2\varphi)/r^2\delta/(\delta\theta)+(cos^2\thetacos^2\varphi)/r^2\delta^2/(\delta\theta^2)+(cos^2\thetacos\varphisin\varphi)/(r^2sin^2\theta)\delta/(\delta\varphi)-(cos\thetacos\varphisin\varphi)/(r^2sin\theta)\delta^2/(\delta\theta\delta\varphi)+` `(sin^2\varphi)/r\delta/(\deltar)-(sin\varphicos\varphi)/r\delta^2/(\delta\varphi\deltar)+(sin^2\varphicos\theta)/(r^2sin\theta)\delta/(\delta\theta)-(sin\varphicos\thetacos\varphi)/(r^2sin\theta)\delta^2/(\delta\varphi\delta\theta)+(sin\varphicos\varphi)/(r^2sin^2\theta)\delta/(\delta\varphi)+sin^2\varphi/(r^2sin^2\theta)\delta^2/(\delta\varphi^2)+` `sin^2\thetasin^2\varphi\delta^2/(\deltar^2)-(sin\thetacos\thetasin^2\varphi)/r^2\delta/(\delta\theta)+(sin\thetacos\thetasin^2\varphi)/r\delta^2/(\deltar\delta\theta)-(sin\varphicos\varphi)/r^2\delta/(\delta\varphi)+(sin\varphicos\varphi)/r\delta^2/(\deltar\delta\varphi)` `(cos^2\thetasin^2\varphi)/r\delta/(\deltar)+(cos\thetasin\thetasin^2\varphi)/r\delta^2/(\delta\theta\deltar)-(cos\thetasin\thetasin^2\varphi)/r^2\delta/(\delta\theta)+(cos^2\thetasin^2\varphi)/r^2\delta^2/(\delta\theta^2)-(cos^2\thetasin\varphicos\varphi)/(r^2sin^2\theta)\delta/(\delta\varphi)+(cos\thetasin\varphicos\varphi)/(r^2sin\theta)\delta^2/(\delta\theta\delta\varphi)+` `(cos^2\varphi)/r\delta/(\deltar)+(cos\varphisin\varphi)/r\delta^2/(\delta\varphi\deltar)+(cos^2\varphicos\theta)/(r^2sin\theta)\delta/(\delta\theta)+(cos\varphicos\thetasin\varphi)/(r^2sin\theta)\delta^2/(\delta\varphi\delta\theta)-(cos\varphisin\varphi)/(r^2sin^2\theta)\delta/(\delta\varphi)+cos^2\varphi/(r^2sin^2\theta)\delta^2/(\delta\varphi^2)+` `cos^2\theta\delta^2/(\deltar^2)+(cos\thetasin\theta)/r^2\delta/(\delta\theta)-(cos\thetasin\theta)/r\delta^2/(\deltar\delta\theta)+` `sin^2\theta/r\delta/(\deltar)-(sin\thetacos\theta)/r\delta^2/(\delta\theta\deltar)+(sin\thetacos\theta)/r^2\delta/(\delta\theta)+sin^2\theta/r^2\delta^2/(\delta\theta^2)=` 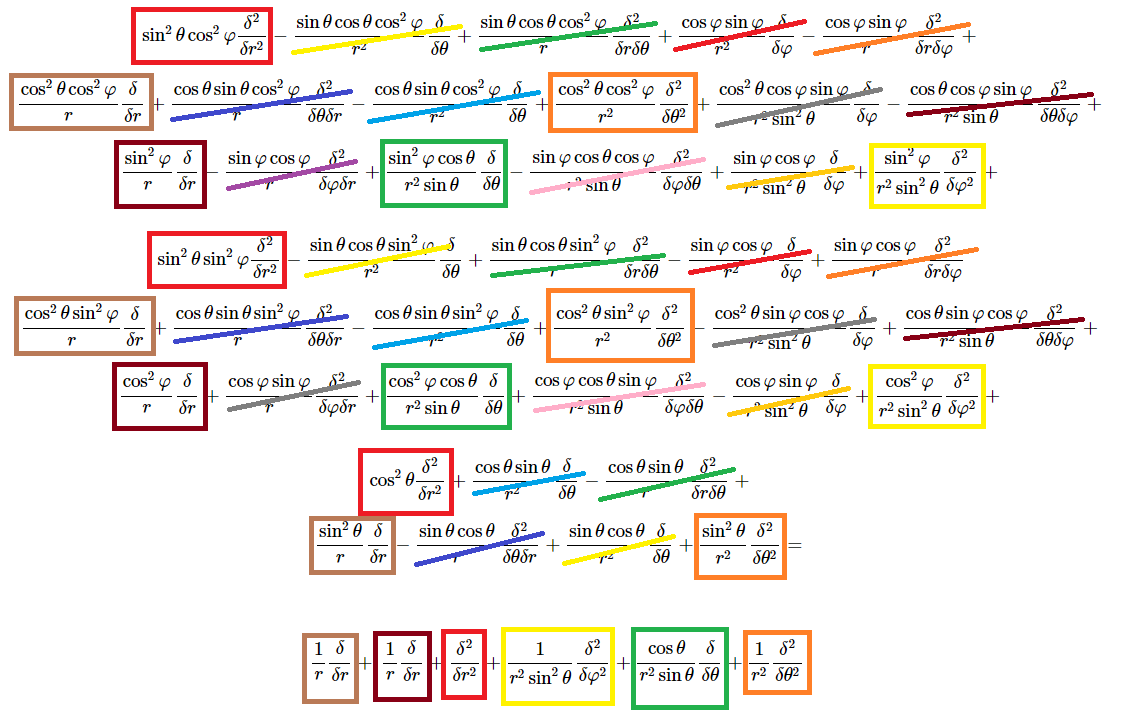 `2/r\delta/(\deltar) + \delta^2/(\deltar^2) + 1/(r^2sin^2\theta)\delta^2/(\delta\varphi^2) + cos\theta/(r^2sin\theta)\delta/(\delta\theta) + 1/r^2\delta^2/(\delta\theta^2) => ` `\nabla^2=1/r^2\delta/(\deltar)(r^2\delta/(\deltar))+1/(r^2sin^2\theta)\delta^2/(\delta\varphi^2)+1/(r^2sin\theta)\delta/(\delta\theta)(sin\theta\delta/(\delta\theta))` (Q.E.D.) Tal com volíem demostrar |