LAPLACIANA 2D EN COORDENADES POLARS Coordenades polars `x=rcos\theta` `y=rsin\theta` `r^2=x^2+y^2` `r=sqrt(x^2+y^2)` `\theta=arctan(y/x)` (recordem que arctan'`(x)=1/(1+x^2)`) En primer lloc calcularem: `(\deltar)/(\deltax)=(2x)/(2sqrt(x^2+y^2))=(rcos\theta)/r=cos\theta` `(\deltar)/(\deltay)=(2y)/(2sqrt(x^2+y^2))=(rsin\theta)/r=sin\theta` `(\delta\theta)/(\deltax)=1/(1+y^2/x^2)ˇ(-y/x^2)=(-y)/(x^2+y^2)=(-rsin\theta)/r^2=(-sin\theta)/r` `(\delta\theta)/(\deltay)=1/(1+y^2/x^2)ˇ(1/x)=x/(x^2+y^2)=(rcos\theta)/r^2=(cos\theta)/r` Anem a calcular `\delta/(\deltax)` i `\delta/(\deltay)` en funció de `\delta/(\deltar)` i `\delta/(\delta\theta)` `\delta/(\deltax)=(\deltar)/(\deltax)\delta/(\deltar)+(\delta\theta)/(\deltax)\delta/(\delta\theta)=cos\theta\delta/(\deltar)-sin\theta/r\delta/(\delta\theta)` `\delta/(\deltay)=(\deltar)/(\deltay)\delta/(\deltar)+(\delta\theta)/(\deltay)\delta/(\delta\theta)=sin\theta\delta/(\deltar)+cos\theta/r\delta/(\delta\theta)` La laplaciana és la suma de les segones derivades parcials. `\nabla^2=\delta^2/(\deltax^2)+\delta^2/(\deltay^2)` `\delta/(\deltax)(\delta/(\deltax))+\delta/(\deltay)(\delta/(\deltay))=` `(cos\theta\delta/(\deltar)-sin\theta/r\delta/(\delta\theta))(cos\theta\delta/(\deltar)-sin\theta/r\delta/(\delta\theta))+ (sin\theta\delta/(\deltar)+cos\theta/r\delta/(\delta\theta))(sin\theta\delta/(\deltar)+cos\theta/r\delta/(\delta\theta))=` `cos\theta\delta/(\deltar)(cos\theta\delta/(\deltar)-sin\theta/r\delta/(\delta\theta)) - sin\theta/r\delta/(\delta\theta) (cos\theta\delta/(\deltar)-sin\theta/r\delta/(\delta\theta)) +` `sin\theta\delta/(\deltar)(sin\theta\delta/(\deltar)+cos\theta/r\delta/(\delta\theta)) + cos\theta/r\delta/(\delta\theta)(sin\theta\delta/(\deltar)+cos\theta/r\delta/(\delta\theta)) =` `cos\theta\delta/(\deltar)(cos\theta\delta/(\deltar)) + cos\theta\delta/(\deltar)(-sin\theta/r\delta/(\delta\theta)) +` `-sin\theta/r\delta/(\delta\theta) (cos\theta\delta/(\deltar))+ sin\theta/r\delta/(\delta\theta) (sin\theta/r\delta/(\delta\theta)) +` `sin\theta\delta/(\deltar)(sin\theta\delta/(\deltar)) + sin\theta\delta/(\deltar)(cos\theta/r\delta/(\delta\theta)) + ` `cos\theta/r\delta/(\delta\theta)(sin\theta\delta/(\deltar)) + cos\theta/r\delta/(\delta\theta)(cos\theta/r\delta/(\delta\theta)) =` `cos^2\theta\delta^2/(\deltar^2) + cos\theta[sin\theta/r^2\delta/(\delta\theta)-sin\theta/r\delta^2/(\deltar\delta\theta)] +` `-sin\theta/r[ -sin\theta\delta/(\deltar)+cos\theta\delta^2/(\delta\theta\deltar)] + sin\theta/r[ cos\theta/r\delta/(\delta\theta)+sin\theta/r\delta^2/(\delta\theta^2)] +` `sin^2\theta\delta^2/(\deltar^2) + sin\theta[-cos\theta/r^2\delta/(\delta\theta)+cos\theta/r \delta^2/(\deltar\delta\theta)] + ` `cos\theta/r[cos\theta\delta/(\deltar)+sin\theta\delta^2/(\delta\theta\deltar)] + cos\theta/r[-sin\theta/r\delta/(\delta\theta) + cos\theta/r\delta^2/(\delta\theta^2)] =` `cos^2\theta\delta^2/(\deltar^2) + (cos\thetasin\theta)/r^2\delta/(\delta\theta)-(cos\thetasin\theta)/r\delta^2/(\deltar\delta\theta) +` `+sin^2\theta/r\delta/(\deltar)-(sin\thetacos\theta)/r\delta^2/(\delta\theta\deltar) + (sin\thetacos\theta)/r^2\delta/(\delta\theta)+sin^2\theta/r^2\delta^2/(\delta\theta^2) +` `sin^2\theta\delta^2/(\deltar^2) -(sin\thetacos\theta)/r^2\delta/(\delta\theta)+(sin\thetacos\theta)/r \delta^2/(\deltar\delta\theta) + ` `cos^2\theta/r\delta/(\deltar)+(cos\thetasin\theta)/r\delta^2/(\delta\theta\deltar) - (cos\thetasin\theta)/r^2\delta/(\delta\theta) + cos^2\theta/r^2\delta^2/(\delta\theta^2) =` 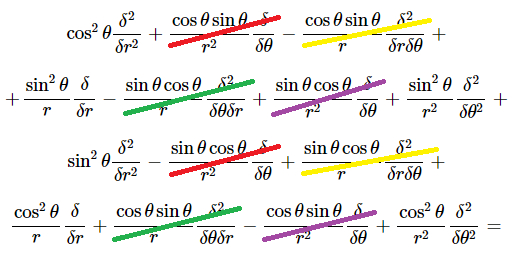`(cos^2\theta+sin^2\theta)\delta^2/(\deltar^2) + (cos^2\theta+sin^2\theta)/r\delta/(\deltar)+ (sin^2\theta+cos^2\theta)/r^2\delta^2/(\delta\theta^2) =` `\delta^2/(\deltar^2) + 1/r\delta/(\deltar)+ 1/r^2\delta^2/(\delta\theta^2)` Laplaciana 2D en coordenades polars: `\nabla^2=\delta^2/(\deltax^2)+\delta^2/(\deltay^2)=\delta^2/(\deltar^2) + 1/r\delta/(\deltar)+ 1/r^2\delta^2/(\delta\theta^2)`