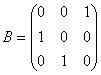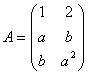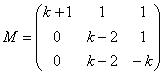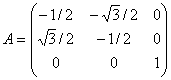|
Matrius i sistemes
Matrius
1. (2009-juny-4) 2. Siguin a) Comproveu que la inversa de A és A2. b) Comproveu també que A518 = B. [1 punt per cada apartat]
2. (2009-juny-3) 1. Considereu la matriu [2 punts]
3. (2009-setembre-1) 1. Considereu la matriu [2 punts]
4. (2010-juny-1) 6. Sigui [2 punts]
5. (2010-juny-4) 2. Considereu la igualtat matricial (A + B)2 = A2+ 2AB + B2 a) Comproveu si les matrius igualtat anterior. b) En general, donades dues matrius qualssevol A i B quadrades del mateix ordre, expliqueu raonadament si hi ha alguna condició que hagin de complir perquè la igualtat de l’enunciat sigui certa. [1 punt per cada apartat]
6. (2010-juny-5) 4. Siguin A, B i C matrius quadrades d’ordre n. a) Expliqueu raonadament si és possible que det A ≠ 0, det B ≠ 0 i det (A · B) = 0. Si és possible, poseu-ne un exemple. b) Si sabem que det A ≠ 0 i que A · B = A · C, expliqueu raonadament si podem assegurar que B = C. [1 punt per cada apartat]
7. (2010-setembre-2) 4. Considereu la matriu a) Comproveu que compleix la igualtat A2 – 5A = I2, on I2 és la matriu identitat d’ordre 2. b) Utilitzeu aquesta igualtat per a calcular la matriu inversa de A. c) Resoleu l’equació matricial [0,5 punts per l’apartat a; 0,75 punts per l’apartat b; 0,75 per l’apartat c]
8. (2011-juny-1) 2. Si tenim la matriu invertible A i l’equació matricial X·A+B=C: a) Aïlleu la matriu X. b) Trobeu la matriu X quan [1 punt per cada apartat]
9. (2011-setembre-2) 1. Donada la matriu a) Calculeu els valors del paràmetre k per als quals la matriu M no és invertible. b) Per a k=0, calculeu M–1.
10. (2011-setembre-2) 4. Sigui la matriu a) Calculeu A2 i A3. b) Deduïu el valor de A101. NOTA: Treballeu amb radicals; no utilitzeu la representació decimal dels elements de la matriu.
|