Teorema del Valor mitjŕ Siguin `f(x)` i `g(x)` dues funcions contínues en `[a , b]` i derivables en `(a , b)`. Existeix un punt `c` que pertany a `(a , b)` tal que: `f'(c)=(f(b)-f(a))/(b-a)` Interpretació geomčtrica: 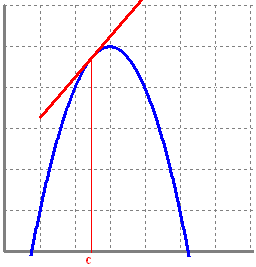Demostració: El teorema de Cauchy diu que: Siguin `f(x)` i `g(x)` dues funcions contínues en `[a , b]` i derivables en `(a , b)`. Existeix un punt `c` que pertany a `(a , b)` tal que: `(f(b)-f(a))/(g(b)-b(a))=(f'(c))/(g'(c))` Si la posem al revés: `(f'(c))/(g'(c))=(f(b)-f(a))/(g(b)-b(a))` Si considerem `g(x) = x` el teorema queda, tenint en compte que `g'(x) = 1` en tot l'interval, (en particular `g'(c) = 1)`: `(f'(c))/1=(f(b)-f(a))/(b-a)` Ja que `g(b)=b` i `g(a)=a` Recordem que `g(x)=x` Quan tenim `f(x)` i `g(x)` dues funcions contínues en `[a , b]` i derivables en `(a , b)`. Existeix un punt `c` que pertany a `(a , b)` tal que: `f'(c)=(f(b)-f(a))/(b-a)`