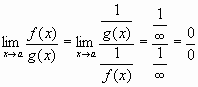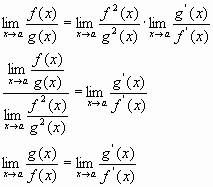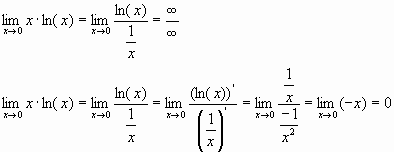|
La derivada i el càlcul de límits. Regla de l'Hôpital a) Siguin f(x) i g(x) dues funcions derivables en un entorn d'a. b) Llavors:
Demostració: Si les funcions són derivables en un entorn d'a vol dir que són contínues en a o sigui:
Llavors (calculem el límit per la dreta):
Per ser derivables f(x) i g(x) en un entorn d'a si agafem x suficientment proper a a es compleixen les condicions per satisfer el teorema de Cauchy la qual cosa implica que existeix un punt c entre x i a tal que:
Ara bé:
Si fem el mateix miran el límit quan x
Exemple d'aplicació de la regla de l'Hôpital: Calcular el
Les funcions x - sin(x) i x són derivables al voltant de 0 (de fet ho són a pertot) per la qual cosa compleixen les condicions per poder aplicar la regla de l'Hôpital.
La regla de l'Hôpital també es pot aplicar en altres situacions: Límits del tipus
Suposem que tenim
Apliquem Hôpital
Que és el mateix que dir
Exemple d'aplicació de la regla de l'Hôpital en le cas d'un límit del tipus
Calcular el
Però el podem canviar
|
i 
i 
a- que procediriem de la mateixa manera acabariem de demostrar el teorema.
.
:
.
