|
Overview -Empieza introduciendo el concepto de área a partir de la de polígonos. -A continuación plantea el problema del cálculo del área del círculo y lo resuelve utilizando el método de exhausción (mediante la suma de las áreas de rectángulos). -Expone el problema del cálculo del área de una figura no poligonal. -Concreta el problema que pretende resolver el cálculo integral. -Define la función área y demuestra gráficamente el teorema fundamental del cálculo. -A continuación explica como se utiliza para contestar a la pregunta que realiza el cálculo integral, regla de Barrow. -Acaba proponiendo unos ejercicios típicos de cálculo de áreas. ÍNDICE
2: Área del círculo 1ª parte 3: Cálculo del área del círculo 2ª parte 4: ¿Cómo calcular el área de cualquier figura? 5: Definición del problema del CÁLCULO INTEGRAL 6: Función área. TEOREMA FUNDAMENTAL DEL CÁLCULO 7: Regla de BARROW 8: Ejercicios
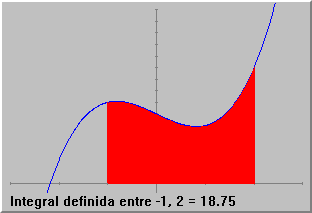
2: Calcula el área bajo la curva f(x)= x3 -2x+6, limitada por x= -1 e x= 2. 3: Calcula el área de la región marcada, limitada por la función f(x)= -x2+2x, entre x = -1 y x = 4. 4: Calcula el área de la región limitada por la función f(x)= -x2+2x+4 y g(x)= x2, entre a = -1 y b = 1.5 . Créditos Versiones
Agradecimientos
Notas -Si quieres un programa que te permite estudiar en profuncidad las funciones, derivadas, integrales, límites,..., pulsa aquí, programa FUNCIONES para Windows. Uno de los programas más utilizados para el estudio de funciones. Es gratuito, a disfrutarlo.  . . |