|
Solució numèrica de l'equació d'Schrödinger independent del temps per a un potencial d'un pou quadrat Física Cuántica "Eisberg-Resnick" (1974-Ed. Limusa) $$ V(x)=\begin{cases} V_0 \qquad x < -\frac{a}{2} \quad \text{o} \quad x > \frac{a}{2}\\ \\ 0 \qquad -\frac{a}{2} < x < \frac{a}{2} \end{cases} $$ $$ \frac{d^2\varphi(x)}{dx^2}=\frac{2m}{\hbar^2}[V(x)-E]\varphi(x) $$ $$ \varphi(x_1)-\varphi(x_0) \approx [\frac{d\varphi(x)}{dx}]_{x_0} (x_1-x_0) $$ $$ \varphi(x_1) \approx \varphi(x_0)+[\frac{d\varphi(x)}{dx}]_{x_0} (x_1-x_0) $$ $$ \frac{d^2\varphi(x)}{dx^2}=\frac{2m}{\hbar^2}[V(x)-E]\varphi(x) $$ $$ d[\frac{d\varphi(x)}{dx}]=\frac{2m}{\hbar^2}[V(x)-E]\varphi(x)dx $$ $$ [\frac{d\varphi(x)}{dx}]_{x_1}-[\frac{d\varphi(x)}{dx}]_{x_0} \approx \frac{2m}{\hbar^2}[V(x)-E]_{x_0}[\varphi(x)]_{x_0}(x_1-x_0) $$ $$ u=\frac{x}{a} $$ $$ [\varphi(u)]_{u_1}=[\varphi(u)]_{u_0}+[\frac{d\varphi(u)}{du}]_{u_0}(u_1-u_0) $$ $$ [\frac{d\varphi(u)}{du}]_{u_1}=[\frac{d\varphi(u)}{du}]_{u_0}+\frac{2ma^2}{\hbar^2}[V(u)-E]_{u_0}[\varphi(u)]_{u_0}(u_1-u_0) $$ $$ \frac{2ma^2V_0}{\hbar^2}=64 $$ $$ E = \alpha V_0 $$ $$ [\frac{d\varphi(u)}{du}]_{u_1}=[\frac{d\varphi(u)}{du}]_{u_0}+[C(u)]_{u_0}[\varphi(u)]_{u_0}(u_1-u_0) $$ $$ C(u)=\begin{cases} \frac{2ma^2}{\hbar^2}[V_0-E]=64(1-\alpha) \qquad u < -0'5 \quad \text{o} \quad u > 0'5\\ \\ -\frac{2ma^2E}{\hbar^2}=-64 \alpha \qquad -0'5 < u < 0'5 \end{cases} $$ $$ [\varphi(u)]_{u_1} = [\varphi(u)]_{u_0} + [\frac{d\varphi(u)}{du}]_{u_0} (u_1 - u_0) $$ $$ [\frac{d\varphi(u)}{du}]_{u_1}=\begin{cases} [\frac{d\varphi(u)}{du}]_{u_0}+64(1-\alpha)[\varphi(u)]_{u_0}(u_1-u_0) \qquad u < -0'5 \quad \text{o} \quad u > 0'5\\ \\ [\frac{d\varphi(u)}{du}]_{u_0}-64\alpha[\varphi(u)]_{u_0}(u_1-u_0) \qquad -0'5 < u < 0'5 \end{cases} $$ Comparació de les gràfiques: 1-(negra) funció d'ona resolta analíticament. 2-(verda) per integració numèrica  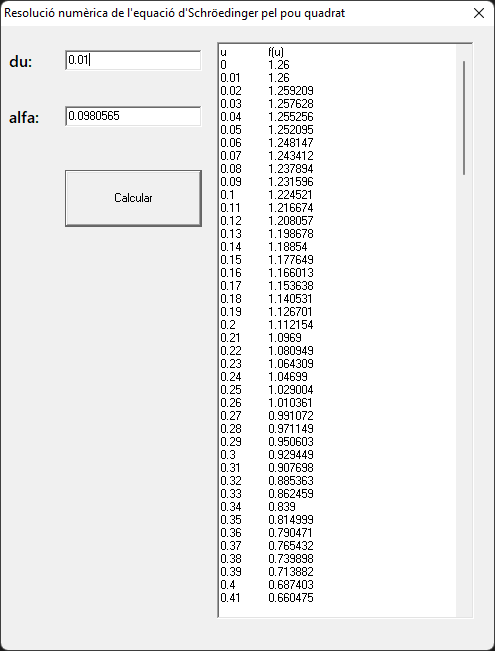 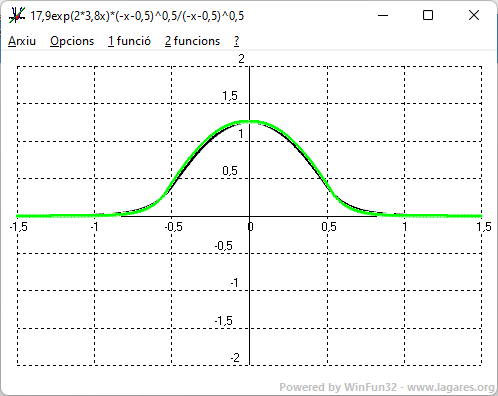 Estimen `C_64` per l'electró e l'àtom d'H. $$ C_{64} = \frac{2ma^2V_0}{\hbar^2} $$ m_\text{electró} = 9'11·10^{-31} \text{ Kg} $$ $$ a = 0'5 · 10^{-10} \quad \text{metres} $$ $$ V_0 = 13'6 \quad \text{eV} · 1'6·10^{-19} \text{ Jouls/eV} = 2'176·10^{-18} \text{ Jouls} $$ $$ \hbar = \frac{6'625·10^{-34}}{2\pi}= 1'054·10^{-34} \quad \text{Jouls·segon} $$ $$ \frac{2ma^2V_0}{\hbar^2}=\frac{2 · 9'11·10^{-31} · (0'5 · 10^{-10})^2 · 2'176·10^{-18}}{(1'054·10^{-34})^2} = 0'892 $$ |