|
Al principi va ser un problema de conills i gallines... ... i ara desitjo entendre el m n. - Un rectangle mesura 130 cm2 de superfície. Calcula quant mesura cada costat si sabem que la base és 3 cm més llarga que l'altura. 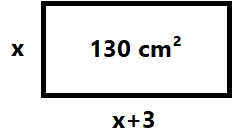 altura `=x` base `=x+3` base altura = rea `x (x+3)=130` `x^2+3x=130` `x^2+3x-130=0` `x=(-3\pm\sqrt{3^2-4 1 (-130)})/2` `x=(-3\pm\sqrt{529})/2` `x=(-3\pm23)/2` `x_1=10` `x_2=-13` Que no considerarem, ja que un costat negatiu no t sentit. altura `=10` `cm` base `=10+3=13` `cm` Que compleix amb les condicions del problema ja que la base s `3` `cm` m s llarga que l'altura i l' rea val `10 13=130` `cm^2` - L'hipotenusa d'un triangle rectangle mesura 39 cm. Quan mesuren els dos catets si sabem que un mesura 21 cm més que l'altre. 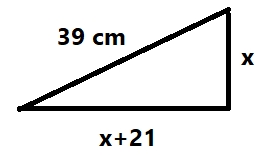 Pel fet de que es tracta d'un triangle rectangle es compleix el teorema de Pit gores `x^2+(x+21)^2=39^2` `x^2+x^2+42x+441=1521` `2x^2+42x-1080=0` `x^2+21x-540=0` `x=(-21\pm\sqrt{21^2-4 1 (-540)})/2` `x=(-21\pm\sqrt{2601})/2` `x=(-21\pm 51)/2` `x_1=(-21+ 51)/2=15` L'altre soluci s negativ i no la tenim en compte ja que no t cap entit una hipotenusa que mesura negatiu. `x=15` `cm` i `x+21=36` `cm` Que podem comprovar que est b ja que aquests dos catets compleixen Pit gores `\sqrt{15^2+36^2} = 39` - He rebut el rebut de la Visa i m'han carregat 96 . vaig comprar uns pantalons i una camisa. No recordo quan valia cada cosa, però si recordo que els pantalons valian el doble que la camisa. Pots ajudar-me a saber quan valia cada cosa? - Troba dos nombres que sumats donin 11 i multiplicats 18. `x+y=11` `x y=18` Podem aillar la `y` en la primera equaci i substituir-ho a la segona. `x+y=11 => y=11-x` `x (11-x)=18` `11x-x^2=18` `0=x^2-11x+18` `x=(11\pm\sqrt{11^2-4 1 18})/2` `x=(11\pm\sqrt{49})/2` `x=(11\pm7)/2` `x_1=9` i `x_2=2 =>` `y_1=11-9=2` i `y_2=11-2=9 =>` Resulta que tenim dues prelles soluci , que s n equivalents `(9,2)` i `(2,9)` O sigui els dos nombres s n `9` i `2` - En un garatge hi ha 132 vehicles. Si hi ha 494 rodes en total (sense comptar amb les de recanvi). Quantes motos i quants de cotxes hi ha? - He comprat a un majorista, ja que tinc una botiga, 64 jerseis i 122 camisetes, n'he pagat 5076 . He de posar-hi uns preus, però no recordo quan valia cada peça, però sí recordo que el preu d'un jersei era 2'5 vegades més car que la camiseta. Quan val un jersei i quan val una camiseta? - Troba dos nombres que sumats donin 102 i restats 26. - He comprat 3 Kg. de peres i 2 Kg. de plàtans que valen 6'7 . Un altre dia compro 3 Kg. de plàtans i 5 Kg. de peres i me costen 10'80 . Quan val un Kg. de peres i un Kg. de plàtans?  Explicaci - Hem comprat un kg de meló que costa 4 . Per pagar-ho hem fet servir monedes de 20 cèntims i de 50. Si en total hem pagat amb 11 monedes, calcula quantes de cada classe hem pagat? - Calcula les dimensions d'un terreny amb forma rectangualar si sabem que la base és tres vegades més gran que l'altura i el perímetre total mesura 64 metres. - Troba dos nombres que multiplicats donin 8'28 i sumats 5'9. `x y=8,28` `x+y=5,9` Fem una substituci : `x=5,9-y` `(5,9-y)y=8,28` `5,9y-y^2=8,28` `0=x^2-5,9y+8,28` `x=(5,9\pm\sqrt{(-5,9)^2-4 1 8,28})/2` `x=(5,9\pm\sqrt{1,69})/2` `x=(5,9\pm1,3)/2` `x_1=3,6` i `x_2=2,3 =>` `y_1=5,9-3,6=2,3` i `x_2=5,9-2,3=3,6` Igual que en el problema anterior trenim dos parells de solucions equivalents: `(3'6,2'3)` i `(2'3,3,6)` O sigui els dos nombres s n `3,6` i `2,3` - Les edats d'en Bernat i el seu pare sumen 49 anys. D'aquí 10 anys l'edat del pare serà el doble de la d'en Bernat. Calcula quants anys tenen ara. - Un fabricant de llanternes obté un benefici de 0'4 per cada llanterna que surt de la fàbrica per vendre, però té una pèrdua de 0'8 per cada llanterna defectuosa que ha de retirar. En una dia ha fabricat 3000 llanternes i ha obtingut uns beneficis nets de 564 . Quantes llanternes aptes per a la venda i quantes llanternes defectuoses ha fabricat? - Una empresa que embotella oli ha omplert 4600 litres en 1400 ampolles de dos i cinc litres. Quantes ampolles de cada classe ha necessitat? - Un examen tipus test de 40 preguntes s'avalua de la següent manera: 0'75 punts per cada resposta correcta i -0'25 per cada resposta errònia. Si un alumne ha tret 18 punts, quantes repostes errònies i respostes correctes ha obtingut? - Una empresa ha de fabricar un nombre de galledes en un cert nombre de dies. Si fabriquen cada dia 300 galledes, en faltaran 500 i si en fabriquen 320 cada dia, en sobraran 100. Quants dies tenen per fabricar les galledes i quantes n'han de fabricar en total? - Un fabricant de vi ha barrejat dues classes de vi, un de 2'5 /litre i l'altra de 4 /litre. Ha obtingut 20 hl d'un vi que costa 3'1 /l. Quants litres de cada clase de vi ha barrejat? - Una empresa de refinatge compra petroli a dos països diferents que anomenem A i B. Comprant 500 barrils al país A i 1.500 al país B el preu mig del barril de cru és de 17 Dolars. Comprant 1.000 barrils al país A i 1.000 barrils al país B el preu mig del barril de cru és de 18 Dolars. Quant costa el barril del país A i quant el barril del país B?. - La Neus ha comprat un abric amb un descompte del 10% i una camisa amb un descompte del 20%. Si ha pagat 56'2 i originament valia tot plegat 65 . Quin era el preu de cada prenda? - La base gran d'un trapezi mesura 4 cm més que la petita. Si l'altura mesura 6 cm i l'àrea 72 cm2. Quant mesuren les bases? - Un tren que circula a 80 Km/h porta una avantatge de 200 Km a un altre que va a 120 Km/h. Quan trigarà el segon a atrapar al primer i quina distància haurà recorregut? - La suma de les dues xifres d'un nombre val 11. Si invertim les xifres resulta un altre nombre igual al triple de l'anterior més 5. De quin nombre es tracta? - Calcula dos nombres la diferència dels quals és 6 i la diferència dels seus quadrats és 120. - Uns diners en un banc durant un any han produït uns interesos de 400 . S'hagués obtingut els mateixos interessos si hi haguéssim posat 5000 més amb un rèdit anual disminuït un 4%. Quin és el capital posat i quin % de rèdit ens han donat? - En una parcela de forma rectangular que fa `56` `metres` de perímetre s'hi construeix un jardí, també rectangular, envoltat per un camí de `2` `metres` d'ample. Calcula les dimensions de la parcela sabent que el jardí té `96` `m^2` de superfície. 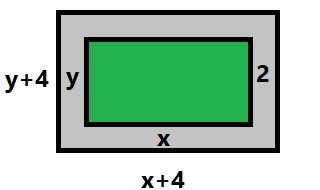 Per metre `= 2 (x+4)+2 (y+4)=2x+2y+16=56 => 2x+2y=40 => x+y=20` rea jard `x y=96` Tenim: `x+y=20` `x y=96` Fem una substituci `y=20-x =>` `x(20-x)=96` `20x-x^2=96` `x^2-20x+96=0` `x=(20\pm\sqrt{(-20)^2-4 96})/2` `x=(20\pm\sqrt{16})/2` `x=(20\pm4)/2` `x_1=12` i `x_2=8` que si calculem les seves `y`, `y_1=8` i `y_2=12` Vol dir dos rectangles equivalents amb el costat curt que mesura `8` i el llarg `12`. recordem que s el rectangle interior, el jard . Per tenir els costats del terreny, cal sumar-li `4` a cada costat del jard : `x=16` `m` i `y=12` `m` 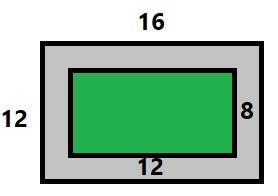 I comprovem que l' rea del jard , interior s: `12 8=96` `m^2` Els següents problemes han estat extrets dels llibres realitzats pel grup de professors anomenat Marea Verde. Als quals agraïm molt el fet de que ens els deixin fer servir. Fem notar que estan escrits en valencià i algunes expressions ens poden semblar un pèl extranyes. - Quin nombre multiplicat per 4 és 5 unitats menor que el seu quadrat? `4x=x^2-5` `0=x^2-4x-5` `x=(4\pm\sqrt{(-4)^2-4 (-5)})/2` `x=(4\pm\sqrt{36})/2` `x=(4\pm6)/2` `x_1=5` i `x_2=-1` Comprovaci : `5 4=5^2-5 => 20=20` i `-1 4 = (-1)^2-5 => -4=-4` - En una classe decideixen que tots enviaran una carta a la resta de companys. Un diu: Escriurem 380 cartes! Calcula el nombre d alumnes que hi ha a la classe. Si hi han `n` alumnes vol dir que cada alumne escriura a `n-1` alumnes, ja que no escriuen cartes a si mateixos. `n (n-1)=380` `n^2-n=380` `n^2-n-380=0` `n=(1\pm\sqrt{(-1)^2-4 1 (-380)})/2` `n=(1\pm\sqrt{1521})/2` `n=(1\pm\39)/2` `n=20` L'altre soluci s negativa i no t cap sentit. Comprovaci , `20` alumnes que escriuen `19` cartes cadasc `20 19=380` cartes. - Calcula tres nombres consecutius tals que la suma dels seus quadrats siga 365. Tres nombres consecutius ser n: Si li diem `n` al primer, doncs `n+1` al segon i `n+2` al tercer. Per la qual cosa si els sumem els seus quadrats: `n^2+(n+1)^2+(n+2)^2=365` `n^2+n^2+2n+1+n^2+4n+4=365` [recorda `(a+b)^2=a^2+2ab+b^2`] `3n^2+6n+5=365` `3n^2+6n+5-365=0` `3n^2+6n-360=0` [Podem dividir tot per `3`] `n^2+2n-120=0` `x=(-2\pm\sqrt{2^2-4 1 (-120)})/2` `x=(-2\pm\sqrt{484})/2` `x=(-2\pm\22)/2`
`x_2=(-2-22)/2=-12` Qu f cilment podem comprovar que compleixen la condici demanada:
- Una fotografia rectangular mesura 14 `cm` de base i 10 `cm` d altura. Al voltant de la foto hi ha un marge de la mateixa amplària per a la base que per a l altura. Troba l ample del marge, sabent que l àrea total de la foto i el marge és de 252 `cm^2`. 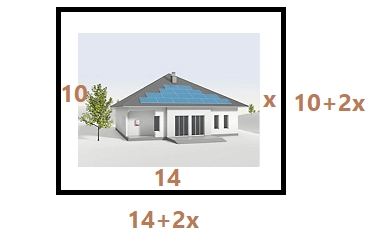
`140+28x+20x+4x^2=252` `4x^2+48x+140-252=0` `4x^2+48x-112=0` `x^2+12x-28=0` `x=(-12\pm\sqrt{12^2-4 1 (-28)})/2` `x=(-12\pm\sqrt{256})/2` `x=(-12\pm16)/2` Per comprovar-hoi cap calcular l' rea del nou rectangle de base `=14+2 2=18` i altura `=10+2 2=14 => 18*14 = 252` `cm^2` - El triple del quadrat d un nombre augmentat en el seu doble és 85. Quin és el nombre?
`3x^2+2x-85=0` `x=(-2\pmsqrt{2^2-4 3 (-85)})/(2 3)` `x=(-2\pmsqrt{1024})/6` `x=(-2\pm32)/6` `x_1=(-2+32)/6=5` `x_2=(-2-32)/6=-34/6` Agafem el `5`. Comprovaci : `3 5^2+2 5 = 85` L'altre `3*(-34/6)^2+2*(-34/6) = 85` - Un triangle isòsceles té un perímetre de 20 cm i la base mesura 4 cm, calcula els costats del triangle i la seua àrea. Com s un triangle is sceles, la suma dels dos costats iguals ha de mesurar, `20-4=16`. Per la qual cosa cada costat ha de mesurar, `16/2=8`. 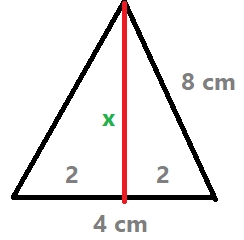 Per trobar l'altua, podem fer servir Pit gores. `x^2+2^2=8^2 => x^2+4=64 => x^2=60 => x=\sqrt{60}` rea `=(\text{base} \text{altura})/2 = (4 \sqrt{60})/2 \approx 15,49` `cm^2` - Un full de paper quadrat es doblega per la meitat. El rectangle resultant té una àrea de `8` `cm^2`. Quin és perímetre del dit rectangle? 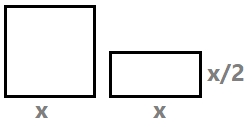
`x^2=16` `x=\sqrt{16} =4` - Un pare diu: "El producte de l edat del meu fill fa 5 anys pel de la seua edat fa 3 anys és la meua edat actual, que són 39 anys". Calcula l edat del fill.
`(x-5) (x-3)=39` `x^2-5x-3x+15=39` `x^2-8x-24=0` `x=(8\pmsqrt{(-8)^2-4 1 (-24)})/2` `x=(8\pmsqrt{160})/2` `x=(8\pm12,65)/2` - Troba les dimensions de rectangle l àrea del qual és `21` `m^2`, sabent que els seus costats es diferencien en 4 metres. 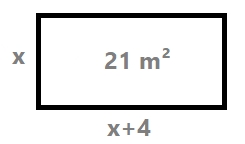
`x^2+4x-21=0` `x=(-4\pm\sqrt{(-4)^2-4 1 (-21)})/2` `x=(-4\pm\sqrt{100})/2` `x=(-4\pm10)/2 = (-4+10)/2=3` - En un triangle rectangle el catet major mesura 3 cm menys que la hipotenusa i 4 cm més que l altre catet. Quant mesuren els costats del triangle?
`(x+3)^2=x^2+(x-4)^2` `x^2+6x+9=x^2+x^2-8x+16` `0=x^2+x^2-x^2-6x-8x+16-9` `x^2-14x+7=0` `x=(14\pm\sqrt{(-14)^2-4 1 7})/2` `x=(14\pm\sqrt{168})/2` `x=(14\pm12,96148)/2` `x1=(14+12,96148)/2 = 13,48074` L'altre soluci :
no la podem tenir en compte ja que l'altre catet mesuraria `0,51926-4 = -3,48074` Catet gran `=13,48074` `cm` Catet petit `=13,48074-4 = 9,48074` `cm` Comprovaci :
- Troba dos nombres parells consecutius el producte dels quals siga 224.
`x(x+2)=224` `x^2+2x-224=0` `x=(-2pm\sqrt{2^2-4 1 (-224)})/2` `x=(-2pm\sqrt{900})/2` `x=(-2pm30)/2` `x_1=(-2+30)/2=14` `x_2=(-2-30)/2=-16` Si considerem els negatius com a parell v lids `x_1=-16` i `x_2=-14` Comprovaci :
- Troba tres nombres imparells consecutius tals que si al quadrat del major se li resten els quadrats dels altres dos s obté com resultat 15.
`(x+4)^2-(x+2)^2-x^2=15` `x^2+8x+16-x^2-4x-4-x^2=15` `-x^2+4x-3=0` `x=(-4pm\sqrt{4^2-4 (-1) (-3)})/-2` `x=(-4pm\sqrt{4})/-2` `x=(-4pm2)/-2` `x_1=(-4+2)/(-2) = 1` `x_2=(-4-2)/(-2) = 3` Hi ha dos de solucions: Comprovaci :
`7^2-5^2-3^2 = 15` Per saber-ne +: Per entendre perqu ara hi han dues solucions v lides, podem representar la funci : I veure que hi ha dos llocs que agafa el valor `15` 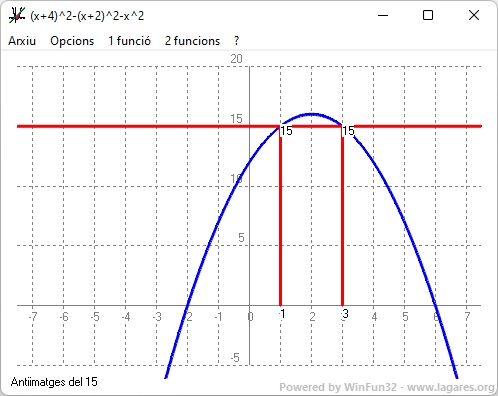 - La suma de les edats de Maria i Alfons són 65 anys. L edat d Alfons menys la meitat de l edat de Maria és igual a 74. Quina edat tenen cadascú?
`y-x/2=74` A llem `y` a la segona equaci , m tode de substituci : `y=x/2+74`
`x+x/2=65-74` `x+x/2=-9` `2x+x=-18` `3x=-18 => x=-18/3=-6` (Maria) i `y=-6/2+74=71` (Alfons) Que evidentment sumen `71+(-6)=65` I si a l'edat de l'Alfons li restem la meitat de la de la Maria `71-(-6)/2=64` Que evidentment s un resultat absurd, excepte que l'Alfons nasqu s d'aqu `6` anys i els dos germans es puguessin portar, `77` anys. - La suma de les edats de Mariló i Xavier és 32 anys. D ací a 7 anys, l edat de Xavier serà igual a l edat de Mariló més 20 anys. Quina edat té cada un en l actualitat?
`y+7=x+7+20` `x+y=32 => y=32-x` `y+7=x+7+20 => y=x+20` Fem un igualaci :
`x+x=32-20` `2x=12` `x=12/2=6` Edat Maril `x=6` i edat Xavier `y=32-x=32-6=26` - Troba dos nombres la diferència dels quals siga 24 i la seua suma siga 104.
`x+y=104` Si sumem les dues equacions
`2x=128` `x=128/2=64` i `64+y=104 => y=104-64=40`
- Un hotel té 42 habitacions (individuals i dobles) i 62 llits, quantes habitacions té de cada tipus? `x` nombre d'habitacions indviduals (`1` llit) i `y` nombre d'habitacions dobles (`2` llits)
`x+2y=62` Restem a la segona equaci la primera
`y=20` i `x+20=42 => x=42-20=22` - En un triangle rectangle la hipotenusa mesura 10 cm i les longituds dels seus dos catets sumen 14 cm. Calcula l àrea del triangle. 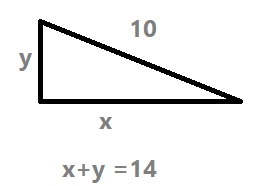
`x^2+y^2=10^2` Podem aillar la `y = 14-x` de la primera equaci i substiituir-la a l'altra. `x^2+(14-x)^2=10^2` `x^2+14^2-28x+x^2=100` `x^2+196-28x+x^2-100=0` `2x^2-28x+96=0` `x^2-14x+48=0` `x=(14pm\sqrt{(-14)^2-4 1 48})/2` `x=(14pm\sqrt{4})/2` `x_1=(14+2)/2 = 8`i `x_2=(14-2)/2 = 6` | `y_1=14-8=6` i `y_2=14-6=8` Tenim una soluci doble, que s la mateixa: `(8,6)` i `(6,8)` Els catets mesuren `8` `cm` i `6` `cm` Comprovaci : `8+6=14` i `8^2+6^2=64+36=100=10^2` - Neus li pregunta a Miriam per les seues qualificacions en Matemàtiques i en Llengua. Miriam li diu "La suma de les meues qualificacions és 19 i el producte 90". Neus li dóna l enhorabona. Quines qualificacions va obtindre? `x` qualificaci de Matem tiques i `y` la de Llengua
`x y=90` `y=19-x` `x(19-x)=90` `19x-x^2=90` `0=x^2-19x+90` `x=(19pm\sqrt{(-19)^2-4 90})/2` `x=(19pm\sqrt{1})/2` `x=(19pm1)/2` `x_1=(19+1)/2 = 10` i `x_2=(19-1)/2 = 9` que dona respectivament `y_1=19-10=9` i `y_2=19-9=10` Comprovaci : `10+9=19` i `10*9 = 90` - D un nombre de tres xifres se sap que sumen 12, que la suma dels seus quadrats és 62, i que la xifra de les desenes és igual a la de les centenes més 1. Quin nombre és? s un problema de 3 inc gnites, `x` xifra de les centenes, `y` xifra de les desenes i `z` xifra d eles unitats.
`x^2+y^2+z^2=62` `y=x+1` Podem substituir la tercera equaci en les altres dues i ens quedar un sistema amb dues inc gnites:
`x^2+(x+1)^2+z^2=62` `2x+z=12-1` `x^2+x^2+2x+1+z^2=62` `2x+z=11` `2x^2+2x+z^2=62-1` A la primera equaci podem a llar la `z`, `z=11-2x` i substituir-la a la segona equaci :
`2x^2+2x+121-44x+4x^2=61` `6x^2-42x+60=0` `x^2-7x+10=0` `x=(7pm\sqrt{(-7)^2-4 10})/2` `x=(7pm\sqrt{9})/2` `x=(7pm3)/2` `x_1=(7+3)/2 = 5 =>` `z=11-2x=11-2*5 = 1 =>` `y=x+1=5+1 = 6 =>`
La suma dels quadrats `5^2+6^2+1^2 = 62` I la xifra de les desenes `6 ` s igual a la de les centenes `5+1` Compte, per l'equaci de segon grau tenia una segona soluci :
Comprovaci :
La suma dels quadrats `2^2+3^2+7^2 = 62` I la xifra de les desenes `3 ` s igual a la de les centenes `2+1` - Es tenen tres sucs compostos de la manera següent: . El primer de 40 dl de taronja, 50 dl de llima i 90 dl de pomelo. . El segon de 30 dl de taronja, 30 dl de llima i 50 dl de pomelo. . El tercer de 20 dl de taronja, 40 dl de llima i 40 dl de pomelo. Es demana quin volum haurà de prendre s de cada un dels sucs anteriors per a formar un nou suc de 34 dl de taronja, 46 dl de llima i 67 dl de pomelo. Aquest problema s de 3 inc gnites, en principi no s de 4t d'ESO, per per qui estigui interessat mostro una manera de resoldre'l. Es resolt plantejant un sistema de `3` equacions amb `3` inc gnites. Diem `x` ald `dl` de la primera barreja i `y` i `z` de la segona i tercera respectivament. Si volem `34` `dl` de taronja vindr de la taronja de cadascun dels tres compostos. I es fa el mateix per la llima i pel pomelo i tenim les tres equacions.
`49x+30y+40z=46` `90x+50y+40z=67` Aix es podria resoldre per substituci , per exemple, agafar la tercera equaci i a llar la `z`, substituir-la a les altres dues i ens quedaria un sistema de dues inc gnites i ja ho sabriem fer. Tot i aix , ho resoldrem pel m tode d'en Gauss, que no es m s que el m tode de reducci fet de forma ordenada Equaci inicial:
`+49x +30y +40z = +46` `+40x +30y +20z = +34` Canviat l'ordre de les equacions: 1 , 3 .
`+49x +30y +40z = +46` `+90x +50y +40z = +67` Multipliquem la 1 equaci per (-49) i ho sumem a la 2 equaci multiplicada per 40 .
`0x -270y +620z = +174` `+90x +50y +40z = +67` Multipliquem la 1 equaci per (-90) i ho sumem a la 3 equaci multiplicada per 40 .
`0x -270y +620z = +174` `0x -700y -200z = -380` Multipliquem la 2 equaci per 700 i ho sumem a la 3 equaci multiplicada per (-270) .
`0x -270y +620z = +174` `0x +0y +488000z = +224400` Multipliquem la 3 equaci per (-620) i ho sumem a la 2 equaci multiplicada per 488000 .
`0x -131760000y 0z = -54216000` `0x +0y +488000z = +224400` Multipliquem la 3 equaci per (-20) i ho sumem a la 1 equaci multiplicada per 488000 .
`0x -131760000y +0z = -54216000` `0x +0y +488000z = +224400` Multipliquem la 2 equaci per (-14640000) i ho sumem a la 1 equaci multiplicada per (-131760000) .
`0x -131760000y +0z = -54216000` `0x +0y +488000z = +224400` Dividim cada equaci pel coeficient de la seva inc gnita.
`0x +y +0z = 0.411475` `0x +0y +z = 0.459836` SISTEMA COMPATIBLE DETERMINAT. Soluci :
`y = 0,411475` `dl` segon compost `z = 0,459836` `dl` tercer compost - Es venen tres espècies de cereals: blat, ordi i mill. Cada kg de blat es ven per 2 , el de l ordi per 1 i el de mill per 0.5 . Si es ven 200 kg en total i s obté per la venda 150 , quants volums de cada cereal s han venut? Aquet problema te alg n problema, en primer lloc, com en el cas anterior s de tres inc nites, `x` `kg` blat, `y` `kg` ordi i `z` `kg` mill. Segon ens parlen de `kg` i ens demana quants volums :-(. En tercer lloc, i aquest s el m s important nom s ens donen dues informacions, que es venen `200` `kg` i s'obtenen `150` . La qual cosa nom s permet plantejar dues eqquacions amb tres inc gnites i, com a m nim, se'n necessiten tres. Per plantejarem les que tenim.
`2x+1y+0,5z=200` El resultat queda indeterminat ja que hi pot haver-hi infinites combinacions que compleixen amdues equacions. Per si interessa saber com es poot trobar aquestes solucions, com abans, ho farem pel m tode de Gauss.
`+2x +y +0.5z = +200` `+x +y +z = +150 ` Canviat l'ordre de les equacions: 1 , 2 . `+x +y +z = +150` `+2x +y +0.5z = +200` Multipliquem la 1 equaci per (-2) i ho sumem a la 2 equaci multiplicada per 1 .
`0x -y -1.5z = -100` Passem les inc gnites no principals a l'altra banda. `+x +y = +150 -z` `0x -y = -100 +1.5z` -x 0y = -50 -0.5z 0x -y = -100 +1.5z +x -0y = +50 +0.5z -0x +y = +100 -1.5z SISTEMA COMPATIBLE INDETERMINAT. Soluci :
y = +100 -1.5z Per veure que hi ha m s d'una soluci nom s cal substituir la `z`, `kg` de mill, pels valors que volem. Per exemple si:
2- `10` `kg` de mill `=> z=10` `=> x=50+0,5*10 = 55` i `y=100-1,5*10 = 85` `(55, 85, 10)` `kg` de cada cosa compleix les condicions. - Es desitja mesclar farina de 2 /kg amb farina d 1 /kg per a obtindre una mescla de 1,2 /kg. Quants kg haurem de posar de cada preu per a obtindre 300 kg de mescla? En direm `x` als `kg` de farina de `2` que mesclarem i `y` als `kg` de farina de `1` . Si volem fer-ne `300` `kg` vol dir que `x+y=300` i el preu d'aquets `300` `kg` ha de ser `300*1,2 = 360` `=>` les equacions seran:
`2x+y=360` Si restem la primera equacio de la segona:
` I si substituim a la primera:
Comprovaci :
i `60 2+240=360=300 1,2` - En una botiga hi ha dos tipus de joguets, els de tipus A què utilitzen 2 piles i els de tipus B que utilitzen 5 piles. Si en total en la botiga hi ha 30 joguets i 120 piles, quants joguets hi ha de cada tipus? Direm que hi ha `a` joguines del tipus A i `b` joguines del tipus B.
`2a+5b=120` Podem a llar `b` a la primera equaci isubstituir-la a la segona.
`2a+5(30-a)=120` `2a+150-5a=120` `-3a=120-150` `-3a=-30` `a=(-30)/-3=10` `b=30-10=20` Comprovaci :
- Un vianant ix d una ciutat A i es dirigeix a una ciutat B que està a 15 km de distància a una velocitat de 4 km/h, i al mateix moment ix un ciclista de la ciutat B a una velocitat de 16 km/h i es dirigeix cap a A, quant temps porta el vianant caminant al moment de la trobada? A quina distància de B s encreuen? En direm `t` al temps de trobada i es trobaran quan la distr ncia recorreguda per tots dos sigui igual a la suma de les dues dist ncies recorregudes que, recordant que l'espai recorregut s `velocitat temps`, el caminador far , `4t` i el ciclista `16t =>`
`20t=15` I l'espai podem calcular-lo mirant la dist ncia recorreguda pel ciclista. Més problemes. Pupurri de tots els tipus: - En una botiga lloguen bicicletes i tricicles. Si tenen 30 vehicles amb un total de 80 rodes, quantes bicicletes i quants tricicles tenen? Direm `x` al n mero de bicicletes que tenen cadascuna `2` rodes i `y` al n mero de tricicles que tenen `3` rodes cascun. El sistema d'equacions que queda, ser :
`2x+3y=80` Farem una substituci :
`2x+3(30-x)=80` `2x+90-3x=80` `-x=80-90` `-x=-10` Comprovaci :
`2*10+3*20 = 80` rodes - Quina és l edat d una persona si en multiplicar-la per 12 li falten 64 unitats per a completar el seu quadrat? Evidentment n'hi direm `x` a l'edat de la persona buscada.
`0=x^2-12x-64` `x=(12pm\sqrt{12^2-4 (-64)})/2` `x=(12pm\sqrt{400})/2` `x=(12pm20)/2` La soluci negativa no tindria massa sentit i ens quede, nom s, amb la positiva Comprovaci :
- Descompon 12 en dos factors la suma dels quals siga 7.
`x+y=7` Provant pocs nombres ja es veu que la soluci s 3 i 4, per resoldrem l'equaci per practicar sistemes de segon grau. Farem uns substituci .
`(7-y)y=12` `7y-y^2-12=0` `-y^2+7y-12=0` `x=(-7pm\sqrt{7^2-4 (-1) (-12)})/-2` `x=(-7pm\sqrt{1})/-2` `x=(-7pm1)/-2` `x_2=(-7-1)/(-2) = 4 => y_2=7-4=3` En resum, `(3,4)` - El triple del quadrat d un nombre augmentat en el seu doble és 616. Quin nombre és?
`3x^2+2x-616=0` `x=(-2pm\sqrt{2^2-4 3 (-616)})/(2 3)` `x=(-2pm\sqrt{7396})/6` `x=(-2pm86)/6` Comprovaci , ens quedarem nom s amb el positiu.
- La suma dels quadrats de dos nombres imparells consecutius és 130. Determina els dits nombres.
`n^2+n^2+4n+4-130=0` `2n^2+4n-126=0` `n^2+2n-63=0` `n=(-2pm\sqrt{2^2-4 (-63)})/2` `n=(-2pm\sqrt{256})/2` `n=(-2pm16)/2` O sigui les dues solucions s n: `(7,9)` i (-9,-7) Comprovaci :
Si considerem que els imparells cal que sigui positius, nom s tindrem en compte el primer parell. M'endescuidava, `7` i `9` efectivament s n imparells. Si no ho haguessin sigut, el problema no hagu s tingut soluci . - Van carregats un ase i un mul. L ase es queixava del pes que portava damunt. El mul li va contestar: Si jo portara un dels teus sacs, portaria el doble de càrrega que tu, però si tu prens un dels meus, els dos portarem la mateixa càrrega. Quants sacs porta cada un? `x` nombre de sacs que porta l'ase i `y` nombre de sacs que porta el mul.
`x+1=y-1` `2x-2=y+1` `x-y=-2` `2x-y=3` `x-y=-2` Si restem la segona equaci a la primera:
I si substituim a la segona:
`5+2=y` `y=7` Comprovaci :
Si l'ase porta un sac del mul en porten `6` tots dos. - Quin nombre multiplicat per 3 és 28 unitats menor que el seu quadrat?
`x^2-3x-28=0` `x=(3pm\sqrt{(-3)^2-4 (-28)})/2` `x=(3pm\sqrt{121})/2` `x=(3pm11)/2` Comprovaci :
i `3*(-4) = -12 = (-4)^2-28` - Calcula tres nombres consecutius la suma de quadrats dels quals és 110.
`n^2+n^2+2n+1+n^2+4n+4=110` `3n^2+6n+1+4-110=0` `3n^2+6n-105=0` `n=(-6pm\sqrt{6^2-4 3 (-105)})/(2 3)` `n=(-6pmsqrt{1296})/6` `n=(-6pm36)/6` `n_1=(-6+36)/6 = 5` i `n_2=(-6-36)/6 = -7` Comprovaci :
- D ací a 2 anys, l edat de Raquel serà la meitat del quadrat de l edat que tenia fa 10 anys. Quina edat té Raquel?
`2x+4=x^2-20x+100` `0=x^2-20x-2x+100-4` `x^2-22x+96=0` `x=(22pm\sqrt{22^2-4 96})/2` `x=(22pm\sqrt{100})/2` `x=(22pm10)/2` Hi ha dues possibles solucions:
i `x_2=(22-10)/2 = 6` En aquest segon cas l'edat de fa `10` anys no t massa sentit i agafarem l'altra.
- Dos nombres es diferencien en 3 unitats i la suma dels seus quadrats és 185. Quins són els dits nombres? Un nombre `x`, l'altre `x+3`.
`x^2+x^2+6x+9-185=0` `2x^2+6x-176=0` `x^2+3x-88=0` `x=(-3pm\sqrt{3^2-4 (-88)})/2` `x=(-3pm\sqrt{361})/2` `x=(-3pm19)/2` `x_1=(-3+19)/2 = 8` i `x_2=(-3-19)/2 = -11` Comprobaci (evidentment es diferencien en tres unitats:
- La suma de dos nombres és 2 i el seu producte és -80, de quins nombres es tracta?
`xy=-80` `y=2-x` `x(2-x)=-80` `2x-x^2=-80` `0=x^2-2x-80` `x=(2pm\sqrt{(-2)^2-4 (-80)})/2` `x=(2pm\sqrt{324})/2` `x=(2pm18)/2` `x_1=(2+18)/2 = 10 => y_1=2-10=-8 => (10,-8)` i `x_2=(2-18)/2 = -8 => y_2=2-(-8)=10 => (-8,10)` Que de fet, s la mateixa soluci . Comprovaci
- Maria vol formar safates d un quilogram amb caramels i bombons. Si els caramels li costen a 3 euros el quilo i els bombons a 7 euros el quilo, i vol que el preu de cada safata siga de 5 euros, quina quantitat haurà de posar de cada producte? Si vol formar 100 safates, quina quantitat de caramels i de bombons necessitarà? `x` kg de caramels i `y` kg de bombons per cada safata que pesa `1` kg.
`3x+7y=5` `y=1-x` `3x+7(1-x)=5` `3x+7-7x=5` `3x-7x=5-7` `-4x=-2` Si vol fer 100 safates vol dir que cales `100 0,5=50` kg de caramels i `50` de bombons - Determina els catets d un triangle rectangle la suma dels quals és 17 cm i la hipotenusa del dit triangle mesura 13 cm. `Catet_1 =x` i `Catet_2=17-x` i com han de complir Pit gores:
`x^2+289-34x+x^2=169` `2x^2-34x+289-169=0` `2x^2-34x+120=0` `x^2-17x+60=0` `x=(17pm\sqrt{(-17)^2-4 60})/2` `x=(17pm\sqrt{49})/2` `x=(17pm7)/2` i `x_2=(17-7)/2 = 5` i `y_2=17-5=12` Que s la mateixa. En resum: els catets mesuren `(12,5)` Comprovaci : `12^2+5^2=169=13^2` i `12+5=17` - El producte de dos nombres és 6 i la suma dels seus quadrats 13. Calcula els dits nombres.
`x^2+y^2=13`
`x^2+(6/x)^2=13` `x^2+36/x^2=13` `x^4+36=13x^2` `x^4-13x^2+36=0`
`t=(13pm\sqrt{(-13)^2-4 36})/2` `t=(13pm\sqrt{25})/2` `t=(13pm5)/2` `t_1=(13+5)/2 = 9` i `t_2=(13-5)/2 = 4` Per trobar `x` cal fer la `\sqrt{}`
Que es f cil veure que el seu producte s `3 2=6` i `3^2+2^2=13` - La suma de dos nombres és 12. El doble del primer més el triple del segon és 31. De quins nombres es tracta?
`2x+3y=31` `x=12-y` `2(12-y)+3y=31` `24-2y+3y=31` `(5,12)` Comprovaci :
`2*5+3*7 = 31` - A un garatge hi ha 30 vehicles entre cotxes i motos. Si en total hi ha 80 rodes, quants cotxes i motos hi ha al garatge? Cal recordar que els cotxes (`x`) tenen `4` rodes i les motos (`y`) `2` rodes.
`4x+2y=80` `y=30-x` `4x+2(30-x)=80` `4x+60-2x=80` `2x=80-60` `2x=20` `x=20/2 = 10` `y=30-10=20` Comprovaci :
`10*4+20*2 = 80` rodes - L edat actual de Lluis és el doble de la de Miriam. D ací a 10 anys, les seues edats sumaran 50. Quants anys tenen actualment Lluis i Miriam? `x` edat de la Miriam. `2x` edat d'en Lluis. `x+10` i `2x+10` les edayts d'aqu a `10` anys respectivament
`3x=50-10-10` `3x=30` Comprovaci : D'aqui `10` anys en tindran `20` i `30` respectivament que sumn `50` - A la meua classe hi ha 25 persones. Ens han regalat a cada xica 3 adhesius i a cada xic 2 xapes. Si en total hi havia 65 regals. Quants xics i xiques som a classe?
`3x+2y=65` (regals). `x` nombre de noies i `y` nombre de nois. `y=25-x` `3x+2(25-x)=65` `3x+50-2x=65` Comprovaci : Hi ha, `15+10=25` persones i `3*15+2*10 = 65` regals - Entre el meu iaio i el meu germà tenen 80 anys. Si el meu iaio té 50 anys més que el meu germà, quina edat té cada un? yayo `x`, meu germ , `x-50`.
`2x=80+50` `2x=130` `x=130/2 = 65` Comprovaci , que evidentment esporten `50` anys i la suma, `65+15 = 80` - Tres entrepans i un refresc costen 8 . Quatre entrepans i dos refrescos costen 12 . Quin és el preu de l entrepà i el refresc? `x`, preu entrep i `y`, preu refresc.
`4x+2y=12` `-6x-2y=-16` `4x+2y=12` `3 2+y=8` `6+y=8 => y=8-6=2 ` refresc Comprovaci :
`4*2+2*2 = 12` - A una granja hi ha gallines i ovelles. Si es compten els caps, són 40. Si es compten les potes, són 100. Quants gallines i ovelles hi ha a la granja? `x` n mero de gallines amb `2` potes i `1` cap cadascuna `y` n mero d'ovelles amb `4` potres i `1` cap cadascuna.
`2x+4y=100` `y=40-x` `2x+4(40-x)=100` `2x+160-4x=100` `2x-4x=100-160` `-2x=-160` `x=40-30=10` ovelles Comprovaci :
- Un rectangle té un perímetre de 180 metres. Si el llarg és 10 metres major que l ample, quines són les dimensions del rectangle? Si el costat curt mesura `x` metres i el llarg `x+10` tenein en compte que hi ha `2` costat de cada i la suma de ttos ells s el per metre, l'equaci pot quedar:
`2x+2x+20=180` `4x=180-20` `4x=160` `x=160/4 = 40` metres el costat curt i `40+10=50` metres el costat llarg. Comprovaci : `40+50+40+50 = 180` metres de per metre - A un portamonedes hi ha bitllets de 5 i 10 . Si en total hi ha 10 bitllets i 75 , quants bitllets de cada valor hi ha al portamonedes? `x` nombre de bitlles de `5` i `y` nombre de bitllets de `10`
`5x+10y=75` `-5x-5y=-50` `5x+10y=75` `5y=25` `x+5=10 => x=10-5=5` bitllets de `5` Comprovaci :
`5*5+5*10 = 75` en total - A una baralla entre aranyes i vespes, hi ha 13 caps i 90 potes. Sabent que una aranya té 8 potes i una vespa 6, quantes vespes i aranyes hi ha a la baralla? `x` nombre d'aranyes i `y` nombre de vespes.
`8x+6y=90` `y=13-x` `8x+6(13-x)=90` `8x+78-6x=90` `2x=90-78` `2x=12` `y=13-6=7` vespes Comprovaci :
`6*8+7*6 = 90` potes - Una classe té 30 estudiants, i el nombre de xiques és doble que el de xics, quants xics i xiques hi ha? `x` nombre de xics i `2x` nombre de xiques
`3x=30` `x=30/3=10` xics i `2 10=20` xiques Comprovaci : `10+20 = 30` estudiants - Neus té 9 anys més que el seu germà Daniel, i sa mare té 50 anys. D ací a 2 anys l edat de la mare serà doble de la suma de les edats dels seus fills, quines edats tenen? `x` edat d'en Daniel, `x+9` l'edat de la Neus. D'aqu `2` anys la mare `52` anys, en Daniel `x+2` i la Neus `x+11`
`52=2(2x+13)` `52=4x+22` `52-22=4x` `30=4x` `4x=30` `x=30/4=7,5` Comprovaci : D'aqui `2` anys en tindran `9,5` i `16,5` que sumen `9,5+16,5 = 26` que s la meitat de `52`, l'edat de la mare - Es mesclen 18 kg d arròs de 1,3 el quilogram amb 24 kg d arròs de preu desconegut, resultant el preu de la mescla de 1,7 el kg. Quin preu tenia el segon arròs? `x` preu del segon arr s:
`23,4+24x=42 1,7` `24x=42 1,7-23,4` `24x=48` Comprovaci :
`(18+24)*1,7 = 71,4` - L altura d un trapezi isòsceles és de 3 cm, el perímetre, 28 cm, i els costats inclinats són iguals a la base menor. Calcula l àrea del trapezi.  base menor `= x =` costats inclinats. `y =` base triangle
`3^2+y^2=x^2` `2x+y=14` `9+y^2=x^2` `y=14-2x` `9+(14-2x)^2=x^2` `9+196-56x+4x^2=x^2` `4x^2-x^2-56x+205=0` `3x^2-56x+205=0` `x=(56pm\sqrt{(-56)^2-4 3 205})/(2 3)` `x=(56pm\sqrt{676})/6` `x=(56pm 26)/6` L'altra soluci : dona un costat negatiu, o sigui, sense sentit Agafem la primera soluci :  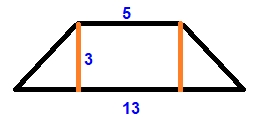 - Dos autobusos ixen, un des de Madrid i l altre des de Càceres a les 9 del matí. Un va a 80 km/h i l altre a 100 km/h. A quina hora s encreuen? A quants km de Madrid estaran? Podr em dir-n'hi `t` al temps que triguen en trobar-se, a la inc gnita, per aquets problema no es pot resoldre, ja no ens donen la dist ncia de Madrid a C ceres. - En un concurs es guanyen 40 euros per cada resposta encertada i es perden 80 per cada fallada. Després de 10 preguntes, Carmela porta guanyats 280 euros. Quantes preguntes ha encertat? En direm `x` al nombre de preguntes encertades i `10-x` a les fallades per la qual cosa podem plantejar una equaci :
`40x-800+80x=280` `120x=280+800` `120x=1080` Comprovaci : `40*9-80*1 = 280` - Paco ha comprat 5 sucs i 4 batuts per 5,7 , després ha comprat 7 sucs i 5 batuts i li han costat 5,9 . Calcula els preus d ambdues coses. `x` preu de cada suc i `y` prewu de cada batut
`7x+5y=5,9` `7(5x+4y=5,7)` `-5(7x+5y=5,9)` `35x+28y=39,9` `-35x-25y=-29,5` `3y=10,4` `5x+4 3,466666=5,7` `5x=5,7-13,86666` `x=(5,7-13,86666)/5 = -1,633332` Comprovaci :
`7*(-1,633332)+5*3,466666 = 5,9` - Quina fracció és igual a 1 quan es suma 1 al numerador i és igual a 1/2 si es suma 2 al denominador? `x` numerador i `y` denominador
`x/(y+2)=1/2` `x+1=y` `2x=y+2` Substituim `y` a la segona equaci
`2x-x=3` `x=3` i `y=3+1 = 4` Comprovaci :
`3/(4+2)=3/6=1/2` - El quocient d una divisió és 3 i el residu és 1. Si el divisor disminueix en 1 unitat, el quocient augmenta en 3 i el residu nou és 1. Trobar el dividend i el divisor. `x`, divident i `y` divisor. Cal recordar que divident = divisor quocient + residu `=> x=y 3+1`
`x=(y-1)(3+3)+1 => x=6y-5` Podem fer el m tode d'igualaci per trobar la `y`
`5+1=6y-3y` `3y=6` `y=6/3 = 2` i `x=3*2+1 = 7` Comprovaci :
Cal dir que el resultat s un xic "absurd" ja que el resultat de la segona divisi mai es diria `6` i `1` de residu, sin , `7` i `0` de residu ja que el divisor s `1` - Dues amigues van anar a pescar. Al final del dia una va dir: "Si tu em dónes un dels teus peixos, llavors jo tindré el doble que tu". L altra li va respondre: "Si tu em dónes un dels teus peixos, jo tindré el mateix nombre de peixos que tu". Quants peixos tenia cada una? `x` nombre de peixos amiga `a` i `y` nombre de peixos amiga `b`.
`x+1=y-1` `2x-2=y+1` `x+2=y` Substituir `y` a la primera equaci
`2x-x=2+2+1` Comprovaci :
Si s al rev s `a` en tindr `6` i `b` tamb . - Calcula les dimensions d un rectangle sabent que la seua àrea és 35 cm2 i el perímetre del qual, 24 cm. `x` el que mesura la base i `y` el que mesura l'altura i recordem que dues bases m s dues atures tenium el per metre i base altura s l' rea.
`x y=35` Fem uns substituci a la segona equaci :
`12x-x^2=35` `0=x^2-12x+35` `x=(12pm\sqrt{(-12)^2-4 35})/2` `x=(12pm\sqrt{4})/2` Si agafem l'arrel `-` `x_2=(12-2)/2=5 => y_2=12-5=7` o sigui `(5, 7)` que s la mateixa Comprovaci : `2*7+2*5 = 24` `cm` de per metre `7*5 = 35` `cm^2` d' rea - Un vianant ix d una ciutat "A" a una velocitat de 4 km/h, i es dirigeix a una ciutat "B" que està a 20 km de la ciutat "A", 30 minuts després ix un ciclista de la ciutat "B" a una velocitat de 20 km/h i es dirigeix cap a "A", quant temps porta el vianant caminant en el moment de la trobada? A quina distància de "B" s encreuen? Per fer-ho m s senzill, com que el ciclista de la ciutat B surt mitja hora m s tard que el que ha sortit de la ciutat A i, aquest, anava a 4 km/h vol dir que ja haur fet 2 km. s a dir quant surt el de B estan a `18` km de separaci i com entre tos dos fan `20+4 = 24` `(km)/h`el temps que trigaran a trobar-se ser : `v=e/t=> t=e/v=> t=18/24=3/4` d'hora (`45')`, com ja portava, A, mitja hora `(30')` des del principi passaran `75'`, o sigui una hora i quart. - Es desitja mesclar oli de 2,7 /l amb un altre oli de 3,6 /l de manera que la mescla resulte a 3 /l. Quants litres de cada classe han de mesclar-se per a obtindre 100 litres de la mescla? Si en diem `x` als litres de mescla del primer oli i `y` als litres del segon, el sistem d'equacions quedar :
`2,7x+3,6y=300` ja que hi ha `100` litres a `3 ` cada litre (`100*3 = 300`) Ho resolem per substituci : `y=100-x` `2,7x+3,6(100-x)=300` `2,7x+360-3,6x=300` `2,7x-3,6x=300-360` `-0,9x=-60` `y=100-66,66666 = 33,33334` litres segon oli Comprovaci :
`2,7*66,66666+3,6*33,33333 = 300` `300/100=3 ` litre de mescla - En intercanviar les xifres d un nombre de dues xifres s obté un altre que és 45 unitats major. Troba el nombre inicial. Recordem que un nombre de dues xifres, per exemple `67` significa `6` desenes i `7` unitats. `67=6 10+7` Per la qual cosa si n'hi diem `x` a la xifra de les desenes i `y` a la xifra de les unitats, el nombre ser `x 10+y` i el nombre intercanviat `y 10+x`. En resum, el sistem quedar :
I aqu descobrim que nom s tenim una equaci amb dues inc gnites, en principi quedar un sistema indeterminat, per com els nombres han de ser naturals a lo millor queda la soluci determinada amb aquesta coondici :
`9y-9x=45` `y-x=5` O sigui seran soluci totes les parelles de n meros, el segon m s gran que el primer de `5` unitats. La qual cosa implica que son soluci : Comprovaci :
`72-27 = 45` `83-38 = 45` `94-49 = 45` La suposici que els nombres han de ser naturals no han fet que la soluci fos determinada, una nica soluci , per , `y=x+5` t m s solucions no enteres que, evidentment, no podem tenir en compte. - La diagonal d un rectangle medeix 25 cm i el perímetre 70 cm. Troba els costats del rectangle. N'hem fet molts de semblants, no cal dibuix. N'hi direm `x` a la base i `y` a l'altura. Recordem que el per metre son dues bases i dues altures, `2x+2y=70` i la diagonal ha de complir el teorema de Pit gores, `x^2+y^2=25^2` i ja tenim el sistema: (simplifiquem un xic i resolem per substituci , ja que s un sistema de segon grau i acostuma a anar b )
`x^2+y^2=625` `y=35-x` `x^2+(35-x)^2=625` `x^2+1225-70x+x^2=625` `2x^2-70x+600=0` `x^2-35x+300=0` `x=(35pm\sqrt{(-35)^2-4 300})/2` `x=(35pm\sqrt{25})/2` `x=(35pm5)/2` i `x_2=(35-5)/2 = 15 => y_2=35-20 = 15` Que s la mateixa soluci Comprovaci
Pit gores `20^2+15^2 = 625=25^2` - Una tanca rodeja un terreny rectangular de 300 `m^2`. Si la tanca medeix 70 metres, calcula les dimensions del terreny. En diem `x` a la base i `y` a l'altura. Com en el problema anterior la tanca, s el per metre, `2x+2y=70 => x+y=35` i recordem que l' rea s base altura `=> x y=300`. El sistema queda, i el resolem per substituci .
`x y=300` `y=35-x` `x(35-x)=300` `35x-x^2=300` `x^2-35x+300=0` `x=(35pm\sqrt{(-35)^2-4 300})/2` `x=(35pm\sqrt{25})/2` `x=(35pm5)/2` Si busquem l'atre soluci podem veure, mireu problema anterior, que s equivalent a aquesta. Comprovaci :
`20*15 = 300` `m^2` - Diversos amics faran un regal de bodes que costa 800 euros, que pagaran a parts iguals. A última hora s apunten sis amics més, amb la qual cosa cada un toca a 30 euros menys. Quants amics eren inicialment? Quant pagarà al final cada un? `x` nombre inicial d'amics i `y` el que havien de pagar al principi.
`(x+6)(y-30)=800` `y=800/x` `x y-30x+6y-180=800` Substituim `x y` i `y`
`-30x+4800/x-180=0` `-x+80/x-6=0` `-x^2+160-6x=0` `x^2+6x-160=0` `x=(-6pm\sqrt{6^2-4 (-160)})/2` `x=(-6pm\sqrt{676})/2` `x=(-6pm26)/2` Agafem la soluci positiviva, ja que la negativa no tindria massa sentit: Comprovaci :
- Les diagonals d un rombe es diferencien en 2 cm i la seua àrea és de 24 `cm^2`. Calcula el seu perímetre. Si una diagonal mesura `x` l'altra `x+2` i l' rea d'un rombe s `(Diagonal diagonal)/2`
`x^2+2x=48` `x^2+2x-48=0` `x=(-2pm\sqrt{2^2-4 (-48)})/2` `x=(-2pm\sqrt{196})/2` `x=(-2pm14)/2` Comprovaci :
- Un tren ix de Barcelona cap a Madrid a una velocitat de 200 km/h. Una hora més tard ix un altre tren de Madrid cap a Barcelona a 220 km/h; la distància entre les dues ciutats és de 618 km. Al cap de quant temps s encreuen els dos trens? A quina distància de Barcelona? El tren de Barcelona, quant surt el de Madrid al cap d'una hora, ja porta `200` km per la qual cosa nom s en falten `618-200 = 418` km. O sigui entre tots dos fan `200+220 = 420` `(km)/h`. Si dividim els `418` km per aquesta velocitat sabrem el temps que trigaran a trobar-se. `t=418/420 \approx 1` hora. s a dir: - Un cotxe ix d una ciutat "A" a una velocitat de 100 km/h i 30 minuts més tard un altre cotxe ix de "A" en la mateixa direcció i sentit a una velocitat de 120 km/h, quant temps tardarà el segon a atrapar al primer i a quina distància de "A" es produeix la trobada? Aquest problema s diferent dels anteriors, ja que tots dos cotxes surten de la mateixa ciutat i ho fan en el mateix sentit. Com el segon cotxe surtmitja hora despr s que el primer i aquest va a `100` `(km)/h` li portar d'avantatge `50` `km` que l'altra cotxe haur de guanyar gr cies a que porta una velocitat, `120-100 = 20` `(km)/h` m s depressa. Per la qual cosa si dividim els `30` km per aquests `20` `(km)/h` sortir el temps que trigar a trobar el segon cotxe al primer cotxe despr s d'haver sortit aquest segon cotxe. `t=30/20 = 1,5` hores. Com el segon cotxe anava a `120` `(km)/h` en aquest temps haur recorregut: |
contador de visitas