Volem construir una peça metàl·lica que tingui per secció un trapezi isòsceles amb la base superior tres vegades més llarga que la base inferior. Els altres costats del trapezi fan `10` mm, tal com podeu observar en la figura següent: 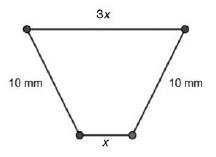a) Expresseu l’altura del trapezi en funció de la longitud `x` de la base inferior. [0,5 punts] Solució: 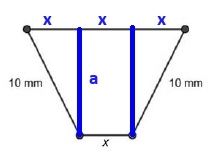Fixeu-vos que tenim un triangle rectangle que ha de complir el teorema de Pitàgores `a^2+x^2=10^2` `a=\sqrt{100-x^2}` b) Calculeu la longitud de la base inferior del trapezi de manera que l’àrea de la peça sigui màxima i trobeu el valor d’aquesta àrea màxima. [2 punts] Solució: Àrea trapeci `A(x)=(a·(B+b))/2 = (a·(3x+x))/2=(a·4x)/2= a·2x= x·\sqrt{100-x^2}=2x·\sqrt{100-x^2}` Per trobar el màxim cal trobar quan la derivada val `0`. `A'(x)=2\sqrt{100-x^2}+2x·1/2·(-2x)/\sqrt{100-x^2}=2\sqrt{100-x^2}-(2x^2)/\sqrt{100-x^2}=0` `2\sqrt{100-x^2}-(2x^2)/\sqrt{100-x^2}=0` `\sqrt{100-x^2}=x^2/\sqrt{100-x^2}` `100-x^2=x^2` `100=2x^2` `50=x^2` `x=+-\sqrt{50}` Que evidentment la solució negativa no té cap sentit `=> x=\sqrt{50}` L'altura val `a=\sqrt{100-x^2}=\sqrt{100-\sqrt{50}^2}=\sqrt{100-50}=\sqrt{50}` L'àrea demanada és `A=(a·2x)=(\sqrt{50}·2\sqrt{50})=2·50=100` `mm^2` Per demostrar que això és un màxim podem trobar el valor de l'àrea en dos punts, un a l'esquerra i l'altre a la dreta, `x=\sqrt{50} \approx 7,071067`. A l'esquerra `x=0` i a la dreta `x=10`. `A(x)=2x·\sqrt{100-x^2} => A(0)=0·\sqrt{100}=0 i A(10) = 10· \sqrt{100-100}=0` Que evidentment són àrees més petites que la que val `100`. Per la qual cosa en `x=\sqrt{50}` l'àrea té un màxim.