La Núria té un jardí rectangular i vol fer-hi un tan-cat (rectangular o quadrat) de `8` `m^2` per al seu gos. Ha pensat de posar el tancat tocant al mur del jardí, tal com es mostra a la figura de la dreta, per estalviar-se així un dels quatre costats. El preu de la tanca que vol fer servir és de `2,5` €/m.


a)Quines dimensions ha de tenir el tancat perquè el cost sigui mínim? Quin és aquest cost mínim? [1,75 punts]

Solució: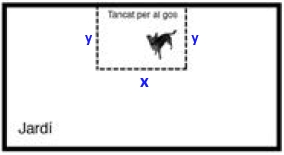

    Si en diem `x` a la part de la tanca horitzontal i `y` a la vertical la funció a optimitzar, preu és el perímetre per `2,5` €/m. Tenint en compte que la part superior no hi ha tanca, ja que hi ha el mur, el perímetre és `2y+x` per la qual cosa la funció a optimitzar, preu és:

    `p(x,y)=(2y+x)·2,5`

    Però com la superfície ha de ser de `8` `m^2` tenim un lligam entre `x` i `y` que és que `x·y=8` (que és l'àrea. `=> y=8/x` la qual cosa fa que la funció a optimitzar sigui:

    `p(x)=(2·8/x+x)·2,5 = 40/x+2,5x= 2,5x+40/x`

    Com volem que aquest preu sigui mínim, cal trobar-lo. Calculem els punts on la derivada sigui `0` i comprovarem que realment es tracta d'un mínim.

    `p'(x)=2,5-40/x^2`

    `2,5-40/x^2=0`

    `2,5=40/x^2`


    `x^2=40/(2,5)`

    `x^2=16 => x=\sqrt{16}=+-4`


    La solució negativa no teé massa sentit i ens centrarem en la positiva `x=4`, cal demostrar que es un mínim. Calcularem la segona derivada i mirarem que dona positiu.

    `p''(x)=(2,5-40x^(-2))'=-40·(-2)x^(-3)=80/x^3`

    Que si substituim per `x=4 => p''(4)=80/4^3>0 =>` que a `x=4, p(x)` té un mínim.

    Acabem l'exercici si `x=4 => y=8/x => y=8/2=2` per la qual cosa les dimensions de la tanca son:

    `x=4` de base i `y=2` d'altura

    Cal comprar `8` metres de tanca ja que hi ha dues altures i una base i el preu `p=2,5*8 = 20` €.


b)Si manteniu la forma rectangular o quadrada del tancat i feu que un dels vèrtexs del jardí coincideixi amb un vèrtex del tancat, quants euros us podeu estalviar? Raoneu com posaríeu el tancat i justifiqueu amb càlculs matemàtics les dimensions de la vos-tra proposta. [0,75 punts]

Solució: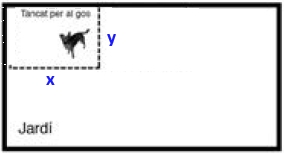
    Ara el preu és `p(x,y)=(x+y)·2,5` i el lligam, l'àrea és el mateix. `x·y=8 => y=8/x`


    `p(x)=(x+8/x)·2,5=2,5x+20/x`

    Si calculem la derivada i la igualem a `0`.

    `p(x)=2,5-20/x^2=0 => 2,5=20/x^2=> x^2=20/2,5 => x^2=8 => x=\sqrt{8}`

    Com abans només tenim en compte la solució positiva. Calculem la segona derivada per comprovar que és un mínim:

    `p''(x)=40/x^3`

    Que si ho substituim per un nombre positiu, `p''(\sqrt{8})=20/(\sqrt{8}^3) >=0`. O sigui a `x=\sqrt{8}` hi ha un mínim.


    I la dimensió `y=8/\sqrt{8}=\sqrt{8}` que resulta que `x` i `y` son iguals el que resulta és que la tanca formarà un quadrat. El cost:

    `p(x,y)=(x+y)·2,5=p(\sqrt{8},\sqrt{8})=(\sqrt{8}+\sqrt{8})·2,5=2\sqrt{8}·2,5 = 14,14213`


    Obtindriem un estalvi de `20-14,14 = 5,86` €.