(2022-juny-2-6)- Al pati d’una escola es vol crear una àrea de joc de `30` `m^2` per als més petits en forma de trapezi rectangular, de manera que la base més gran mesuri el doble que la base més petita, tal com mostra la figura, i que el costat oblic respecte a les bases (D) sigui tan curt com sigui possible. 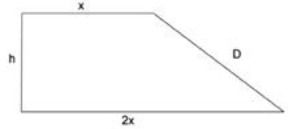a) Justifiqueu que se satisfan les relacions següents: `h=20/x` i `D(x)=\sqrt{400/x^2+x^2}`. [1 punt] b) Trobeu les dimensions del trapezi per a les quals la longitud del costat `D` és mínima. [1,5 punts] SOLUCIÓ: 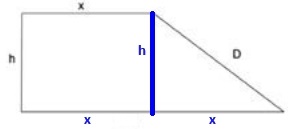a) Àrea trapeci `=((x+2x)·h)/2=(3xh)/2=30 =>` `h=(30·2)/(3x)=20/x` Per Pitàgores `D(x)=\sqrt{h^2+x^2}=\sqrt{(20/x)^2+x^2}=\sqrt{400/x^2+x^2}` b) Per trobar el mínim cal calcular la derivada de `D(x)` i igualar-la a `0` `D'(x)=1/2·(-800/x^3+2x)/\sqrt{400/x^2+x^2}` `(-800/x^3+2x)/(2·\sqrt{400/x^2+x^2})=0` `-800/x^3+2x=0` `2x=800/x^3` `x^4=400` `x=\root(4){400}=4,472135` Per demostrar que és un mínim, podem calcular la derivada a l'esquerra i a la dreta, `D'(4)` i `D'(5)`: `D'(4)=1/2·(-800/4^3+4·2)/\sqrt{400/2^2+2^2}=1/2·(-4,5)/\sqrt{104}<0` `D'(5)=1/2·(-800/5^3+2·5)/\sqrt{400/5^2+5^2}=1/2·(3,6)/\sqrt{41}>0` I tot això és que a l'esquerra de l'extrem, `x \approx 4,472135`, la funció es decreixent, ja que la derivada és negativa i a la dreta, creixent, ja que la derivada és positiva. Tot plegat implica que, en el extrem hi ha un mínim. En resum: `D(4,472135)=\sqrt{400/(4,472135)^2+4,472135^2}=6,324555` | `h=20/(4,472135) = 4,472136` i les mesures demanades són 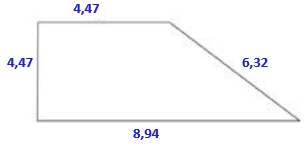NOTA: Podríem haver posat per `x=\root(4){400}=\sqrt{20}=2\sqrt{5}` i `D=D(2\sqrt{5})=\sqrt{400/(2\sqrt{5})^2+(2\sqrt{5})^2}=\sqrt{40}=2\sqrt{10}`