|
(2022-juny-2-4)- a) Trobeu una funció polinòmica `y = g(x)` de grau `3` tal que talli l’eix de les ordenades en el punt `(0, 5)`, que la recta tangent a `y = g(x)` en el punt d’abscissa `x = 1` sigui horitzontal i que `g''(x) = 2x + 1`. [1 punt] b) Comproveu que la funció `f(x) = –x^3 + 6x^2 - 16` té una arrel a `x = 2` i que és estrictament creixent a l’interval `(0, 4)`. Utilitzeu aquesta informació per a calcular l’àrea determinada per la funció `f(x)`, l’eix de les abscisses i les rectes `x = 0` i `x = 4`. [1,5 punts] SOLUCIÓ:
(2) Si la recta tangent en `x=1` és horitzontal `=> g'(1)=0` `g'(x)=3ax^2+2bx+c` `=> g'(1)=3a·1^2+2b·1+c = 3a+2b+c=0` (3) I si `g''(x) = 2x + 1 => g'(x)=6ax+2b=2x+1 =>` Si ho substituim a (2) `3·1/3+2·1/2+c=0 => 1+1+2 =0 => c=-2`
(2) Per demostrar que és estrictament creixent en `(0,4)` cal demostrar que `f'(x)>0` en aquest interval. Recordem que es tracta d'una funció polinòmica que és contínua i derivable en tot `R`. `f'(x)=-3x^2+12x` Això és una paràbola farem el dibuix. Les arrels són `-3x^2+12x=0 => -3x(x-4)=0 => x_1=0` i `x_2=4` El vèrtex de la paràbola `(f'(x))'=0 => f''(x)=0 => f''(x)=-6x+12=0 => x=2` i `f'(2)=-3*2^2+12*2 = 12` podem fer un esbós de la gràfica de `f'(x)` 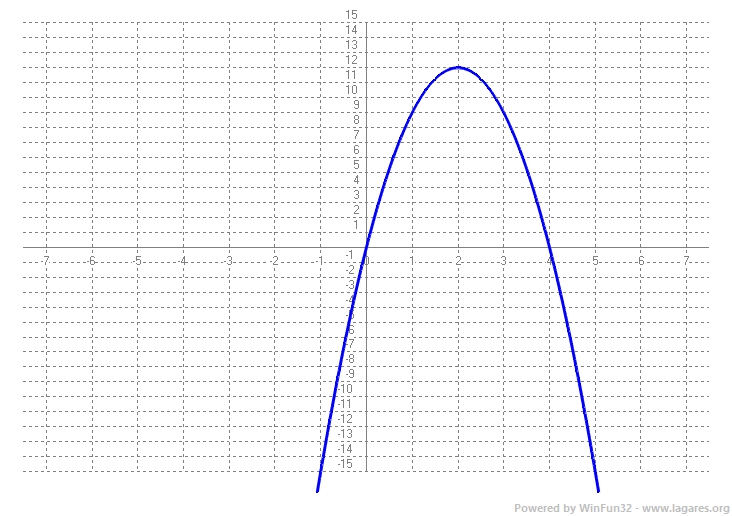 i veiem que a l'interval `(0,4)` (recordem, obert) `f'(x)>0 =>` `f(x)` és estrictament creixent. (3) Com que la funció té una arrel a `2` i és estrictament creixent a `(0,4)` vol dir que per calcular l'àrea entre `0` i `4` caldrà calcular: `|\int_0^2 (–x^3 + 6x^2 – 16) dx|+|\int_2^4 (–x^3 + 6x^2 – 16) dx|=|[-x^4/4+2x^3-16x]_0^2|+|[-x^4/4+2x^3-16x]_2^4|=` `|(-2^4/4+2·2^3-16·2)-(-0^4/4+2·0^3-16·0)|+|(-4^4/4+2·4^3-16·4)-(-2^4/4+2·2^3-16·2)|=` ANNEX: L'exercici no ho demana, però ajudar a entendre que ens demana l'apartt b-3 us mostem la gràfica de l'àrea que acabem de calcular: 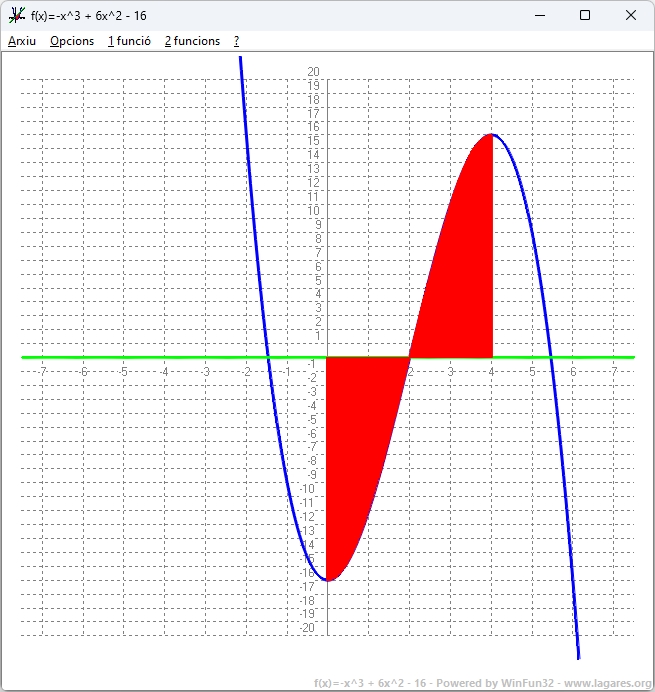 |