17-(2020-setembre-4-3) Sigui `f(x)` una funció derivable la gràfica de la qual passa pel punt `(0, 1)`. La gràfica de la seva derivada, `f'(x)`, és la que es mostra en la figura. 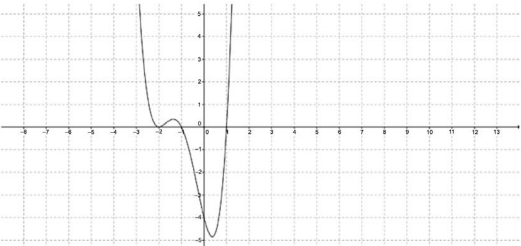a) Calculeu l'equació de la recta tangent a la gràfica de la funció `f(x)` en el punt de la gràfica d'abscissa `x = 0`. b) Trobeu les abscisses dels punts singulars de la funció `f(x)` i classifiqueu-los. a) La recta tangent passa pel `(0,1)` i el pendent val `m=f'(0)=-4` Equació de la recta `y-1=-4(x-0) => y=-4x+1` b) Els punts singulars són aquells que s'anul·la la derivada. `f'(x)=0` en `x=-2`, `x=-1` i `x=1` En `x=0` la funció derivada presenta un mínim per la qual cosa `f''(0)=0` hi ha un possible punt d'inflexió. `f'(x)` a l'esquerra del `0` és decreixent i a la dreta creixent, vol dir que `f''(x)` a l'esquerra del `0` és negativa i a la dreta positiva per la qual cosa `f'''(0)>0 \ne 0 =>` punt d'inflexió. `f''(-1)<0 => f(-1)` hi ha un màxim. `f''(1)>0 => f(1)` hi ha un mínim.