12-(2020-juny-1-6) Considereu la funció `f(x) = x^3`.

a) Calculeu en quin punt del tercer quadrant la recta tangent a `y = f(x)` és paral·lela a la recta `3x - y = 4`. Calculeu l'equació de la recta tangent a la gràfica en aquest punt i feu un dibuix aproximat de la gràfica de la funció i les dues rectes.

b) Calculeu l'àrea de la regió delimitada per `y = f(x)` i la recta `y = 3x + 2`.



a- La recta `3x-y=4 => y=3x-4 => m=3` (pendent). Cal buscar en quin punt del 3r quadrant `f'(x)=3`


    `f'(x)=3x^2 => 3x^2=3 => x=-1, f(-1)=(-1)^3=-1 => (-1,-1)`



Equació de la recta tangent `y-(-1)=3[x-(-1)] => y=3x+2`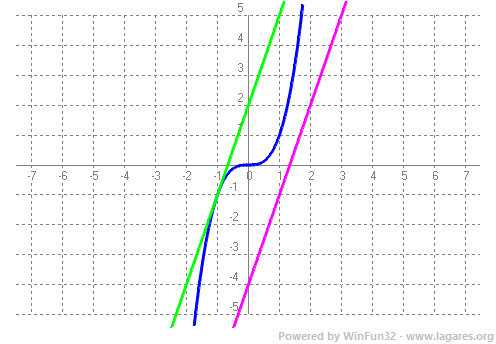






b- Per trobar l'àrea cal trobar els punts de tall.

`x^3=3x+2 => x^3-3x-2=0` com són tangents a `x=-1` sabem que una solució és aquesta.

         |  1   0  -3   -2 
     | 
  -1 |     -1   1    2
-----+------------------------
     |  1  -1  -2    0
     | 
   2 |      2   2
-----+------------------------
        1   1   0


`x^3-3x-2=0 => (x+1)^2·(x-2)`


    Àrea `=\int_(-1)^2 (3x+2-x^3)dx = [(3x^2)/2+2x-x^4/4]_(-1)^2=`


    `(6+4-4)-(3/2-2-1/4)=6-(6/4-8/4-1/4)=6+3/4=24/4+3/4=27/4` `u^2`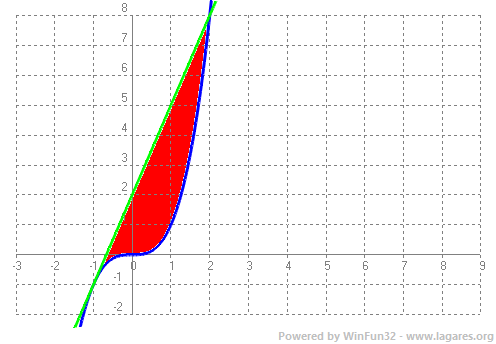