La integral definida `\int_a^bf(x)dx` És l'àrea que queda entre les rectes `x=a`, `x=b` i entre la corva de `f(x) `i l'eix de les `x`. 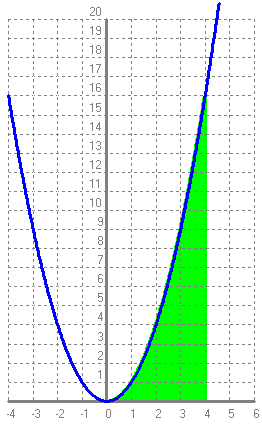En el dibuix anterior: És l'àrea que queda entre les rectes `x=o`, `x=4` i entre la corva de `x^2` i l'eix de les `x`. Podem aproximar l'àrea buscada fent la suma de les àrees dels següents rectangles: 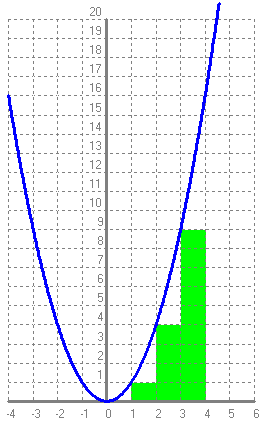Això seria una aproximaxió per defecte. `0·1+1·1+1·4+1·9=14` 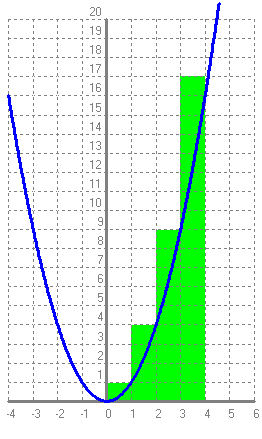Això seria una aproximaxió per excès. `1·1+1·4+1·9+1·16=30` Si fessim els intevals més petits els valors calculats s'acostarien més al valor de l'àrea cercada. Per la qual cosa podem definir la integral definida com: `\int_a^bf(x)dx=lim_(n->+\infty) \sum_(i=1)^n f(x_i)·\Delta x` Exercicis: 1- Calcula, tant per excès, com per defecte, l'àrea entre `x=0`, `x=4`, la funció, `x^2` i l'eix de les `x` fent servir `\Delta x = 0'5`. Quant val `n` en aquest cas?. 2- Calcula, tant per excès, com per defecte, l'àrea entre `x=0`, `x=10`, la funció, `x` i l'eix de les `x` fent servir `\Delta x = 1`. Quant val `n` en aquest cas?. 3- Calcula l'àrea entre `x=0`, `x=10`, la funció, `x` i l'eix de les `x`, fent servir propietats geomètriques del dibuix de la gràfica resultant. 4- Calcula l'àrea entre `x=0`, `x=10`, la funció, `x` i l'eix de les `x`, calculant el `lim_(n->+\infty) \sum_(i=1)^n x_i·\Delta x``.