Introducció. L'antiderivada (primitiva d'una funció), pot ser una cosa útil?



Anem a plantejar dos problemes:


1-El càlcul de l'antiderivada i la cinemàtica.

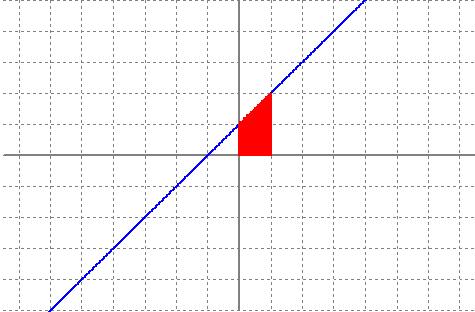
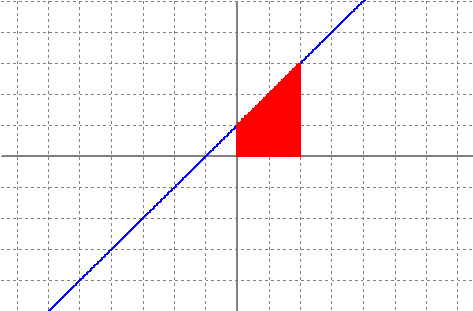
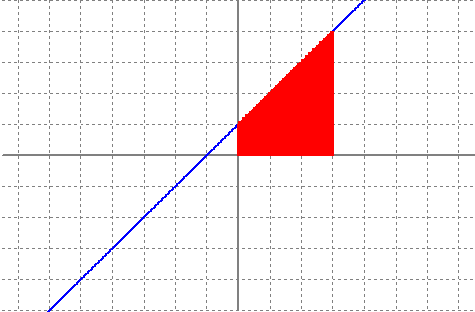
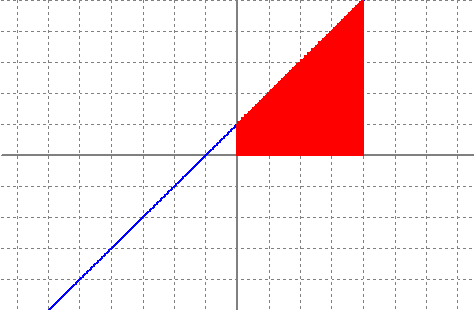
    Quan un cos cau, a física ens diuen, que cau amb una acceleració constant que val uns:

    `9'81 m/s^2` i n'hi diem `g`. Això se'n va donar compta Galileu fa una colla d'anys.


    Però que és la acceleració? És una mesura del canvi en la velocitat, o sigui:


    `a(t)=(d v(t))/(dt)`



    En el cas de que l'acceleració sigui constant i la de la gravetat la fórmula anteriror queda:


    `g = (d v(t))/(dt)`


    O sigui, si l'acceleració és la derivada de la velocitat, la velocitat és l'antiderivada de l'acceleració. Si l'acceleració és constant, per calcular la velocitat només hem de calcular l'antiderivada d'una constant.


    `v(t) = g·t + v_0`


    I què és la velocitat? És una mesura del canvi en la posició `e(t)` (espai en funció del temps), o sigui:


    `v(t)=(d e(t))/(dt)`



    Per la qual cosa i seguint el mateix raonament que a dalt. Si tenim la funció que ens diu la velocitat en funció del temps, només cal antiderivar-la per trobar la l'espai en funció del temps. recordeu que aquí a la vairable independent n'hi diem `t`, en lloc de la `x` tradicional que fem servir a mates.


    `e(t) = 1/2g·t^2 + v_0·t + e_0`


    Si algú no acava de veure lo anterior, agafeu l'expressió de l'espai en funció del temps, `e(t)`, deriveu-la respecte, `t`, i observareu que us dona l'expresió de `v(t)`. Si feu el mateix per `v(t)` veureu que us dona `a(t)=g`.





2-El càlcul de l'àrea sota una funció lineal. Funció àrea desde `0` fins a `x` de la funció `f(x) = x+1`. Càlcul de la seva funció derivada.



`\int_0^1(x+1)dx=1·1+(1·1)/2=1'5`




`\int_0^2(x+1)dx=2·1+(2·2)/2=4`




`\int_0^3(x+1)dx=3·1+(3·3)/2=7'5`




`\int_0^4(x+1)dx=4·1+(4·4)/2=12`

`\int_0^x(x+1)dx=x·1+(x·x)/2=x^2/2+x`

Observeu que:

`(x^2/2+x)'=x+1`


    O sigui la funció àrea,`F(x)=x^2/2+x`, sembla ser l'antiderivada de la funció original, `f(x) = x+1`.