|
Com que `F(x)=G(x)+c` `\int_a^af(t)dt=F(a)=G(a)+c=0 => c=-G(a)` `\int_a^bf(t)dt=F(b)=G(b)-G(a)` 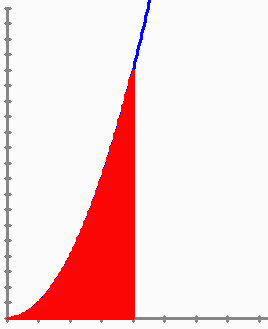 `\int_0^4x^2dx=[x^3/3]_0^4=4^3/3-0^3/3=64/3` |
|
Com que `F(x)=G(x)+c` `\int_a^af(t)dt=F(a)=G(a)+c=0 => c=-G(a)` `\int_a^bf(t)dt=F(b)=G(b)-G(a)`  `\int_0^4x^2dx=[x^3/3]_0^4=4^3/3-0^3/3=64/3` |