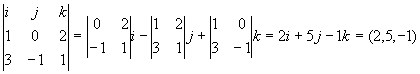Producte vectorial entre dos vectors

Es defineix a partir del càlcul del següent determinant.

El vector resultant té la propietat de que és perpendicular amb els dos primer vectors:

Per comprovar-ho el multipliquem escalarment amb els dos vectors i veiem que dòna 0:

(1, 0, 2) · (2, 5, -1) = 2 + 0 -2 = 0

(3, -1, 1) · (2, 5, -1) = 6 - 5 - 1 = 0

Això ens ofereix una nova manera de calcular la equació general d'un pla:

Exercici: Trobar la equació general del pla:

(x, y, z) = (2, -1, 0) + m(1, 0, 2) + n(3, -1, 1)

Si fem el producte vectorial dels dos vectors directors (2, 5, -1) el que trobem és un vector perpendicular al pla, ho sigui un vector associat. Així l'equació de la recta queda:

2x + 5y - z + D = 0

Per trobar la D l'únic que cal fer és substituir a l'eaució el vector de posició (2, -1, 0)

2·2 + 5·(-1) - 0 + D = 0

-1 + D = 0

D = 1

Finalment l'equació general de la recta queda:

2x + 5y - z + 1 = 0