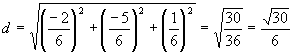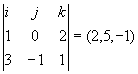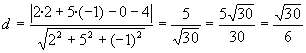Distància entre dues rectes

Ens podem trobar en varis casos:

1-Les dues rectes es tallen en un punt. Com definim la distància com la mínima, evidentment, la distància val 0.

2-Les dues rectes són la mateixa. Com és obvi la distància val 0.

3-Les dues rectes són paral·leles. Llavors podem agafar un punt d'una recta i calcular la distància a l'altra.

4-Les dues rectes es creuen. La distància és el mòdul de l'únic vector que va d'una recta a l'altra i és perpendicular a les dues rectes. Per veure com es calcula la distància ho veurem amb un exercici:

Exercici: Calcular la distància entre els dues rectes següents:

r1: (x, y, z) = (2, -1, 0) + m(1, 0, 2)

r2: (x, y, z) = (0, 1, 1) + n(3, -1, 1)

Les coordenades de qualsevol punt de r1: (2+m, -1, 2m)

Les coordenades de qualsevol punt de r2: (3n, 1-n, 1+n)

Per la qual cosa els vectors que van d'una recta a l'altre tenen la forma:

(2+m, -1, 2m) - (3n, 1-n, 1+n) = (2+m-3n, -2+n, -1+2m-n)

Però de tots aquests vectors el que volem és el que és perpendicular als dos vectors directors. Ho sigui que el producte escalar amb els vectors directors sigui 0.

(2+m-3n, -2+n, -1+2m-n) · (1, 0, 2) = 0

(2+m-3n, -2+n, -1+2m-n) · (3, -1, 1) = 0

2+m-3n-2+4m-2n = 0

6+3m-9n+2-n-1+2m-n =0

5m-5n = 0

5m-11m = -7

La solució d'aquest sistema és:

m = 7/6

n = 7/6

Ho sigui el vector perpendicular a les dues rectes és:

Llavors la distància entre les dues rectes és el mòdul d'aquest vector:

També és pot calcular la distància entre les dues rectes si calculem la distància d'una recta al pla que conté l'altra i és paral·lela a la primera.

Exercici: Calcular la distància entre els dues rectes següents:

r1: (x, y, z) = (2, -1, 0) + m(1, 0, 2)

r2: (x, y, z) = (0, 1, 1) + n(3, -1, 1)

Calculem l'equació del pla que conté a r2 i és paral·lel a r1.

(x, y, z) = (0, 1, 1) + n(3, -1, 1) + m(1, 0, 2)

Calculem l'equació general del pla. Calculem el vector associat a través del producte vectorial dels dos vectors directors:

Ho sigui l'equació general del pla és (Ax + By + Cz + D=0)

2x + 5y - z + D = 0

Per trobar la D, substutuïm pel punt (0, 1, 1).

0 + 5 - 1 + D = 0 => D = -4

En definitiva l'equació de la recta queda:

2x + 5y - z -4 = 0

I la distància d'aquest pla a l'altra recta (que és paral·lela al pla) la calculem calculant la distància del punt (2, -1, 0) al pla utilitzant la fórmula:

Que és el que ens havia donat de l'altra manera.