4-De tots els rectangles inscrits en l'el·lipse `4x^2+y^2=1`, trobeu el que té àrea màxima. 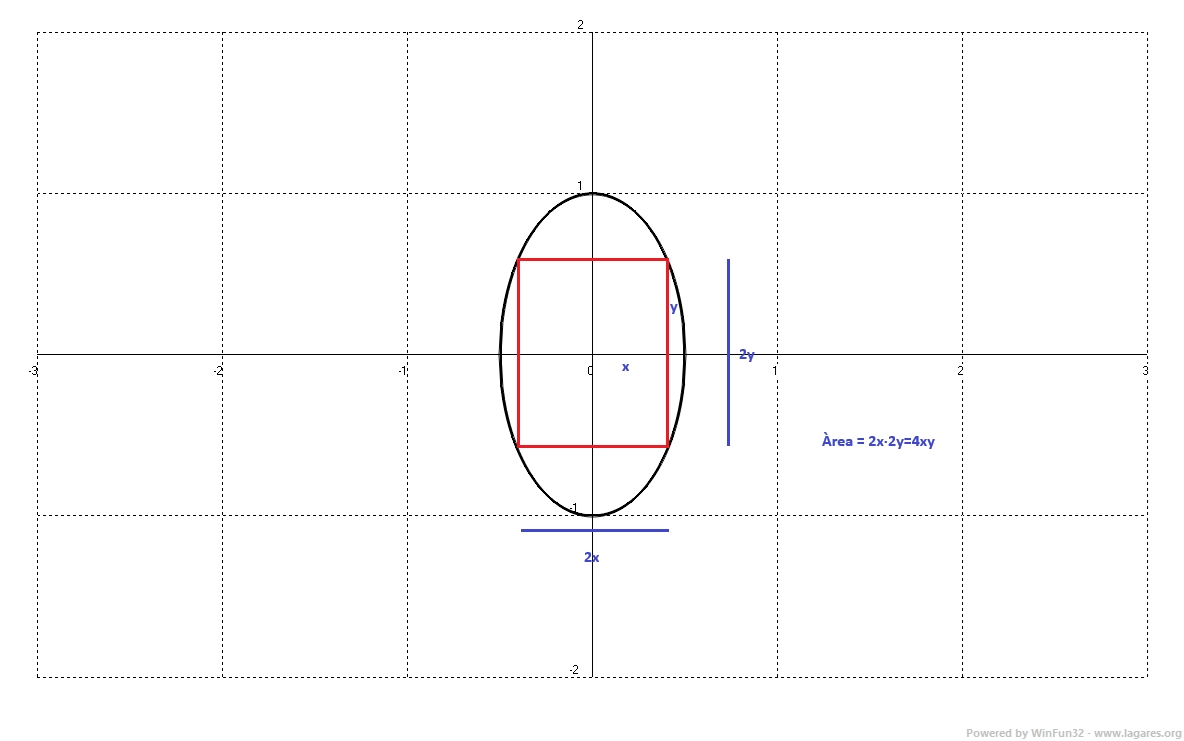`4x^2+y^2=1 => y^2=1-4x^2 => y=\sqrt{1-4x^2}` Trobem el domini de `y`. Els punts de tall amb l'eix de les `x => y=0` `\sqrt{1-4x^2}=0 => 1-4x^2=0 => 1=4x^2 => 1/4=x^2 => x^2=\sqrt{1/4} = \pm 1/2` Només agafem els valos positius de `x` ja que els negatius ens donarien àrees negatives `=> 0<=x<=1/2` Àrea `= A(x) = 4xy = 4x\sqrt{1-4x^2}` Si la derivem per trobar els extrems: `A'(x)=4(\sqrt{1-4x^2}+(x(-8x))/(2\sqrt{1-4x^2}))=4(\sqrt{1-4x^2}-(4x^2)/(\sqrt{1-4x^2}))=4((1-4x^2-4x^2)/(\sqrt{1-4x^2}))=4·(1-8x^2)/(\sqrt{1-4x^2})` `A'(x)=4·(1-8x^2)/(\sqrt{1-4x^2})=0 => 1-8x^2=0 => 8x^2=1 => x^2=1/8 => x=\sqrt{1/8}` I la seva imatge val, Àrea`(\sqrt{1/8})=4·\sqrt{1/8}·\sqrt{1-4(\sqrt{1/8})^2)=4·\sqrt{1/8}·\sqrt{1-4(1/8)}=4·\sqrt{1/8}·\sqrt{1/2}=4·\sqrt{1/16}=4/4=1` `u^2` I ha de ser un màxim, ja que les imatges de `A(0)=0` i `A(1/2)=0` que son els límits del domini que hem trobat abans. Per trobar les dimensions del rectangle trobem la `y` per `x=\sqrt{1/8}`. Recordem que `y=\sqrt{1-4x^2}` `y(\sqrt{1/8})= \sqrt{1-4(\sqrt{1/8})^2)=\sqrt{1-4·1/8}=\sqrt{1-1/2}=\sqrt{1/2}` base `=2x = 2\sqrt{1/8}= \sqrt{4/8}=\sqrt{1/2}` altura `=2y=2\sqrt{1/2}=\sqrt{4/2}=\sqrt{2}` Podem comprovar que si multipliquem base · altura `=\sqrt{1/2}·\sqrt{2}=\sqrt{2/2}=1` `u^2`