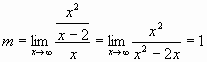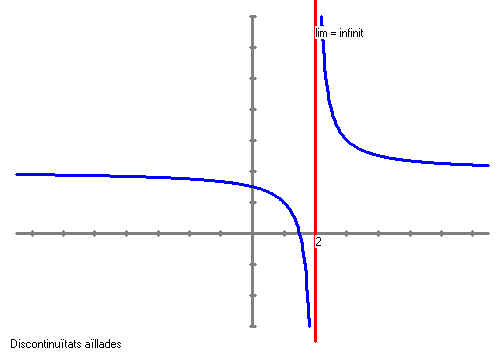
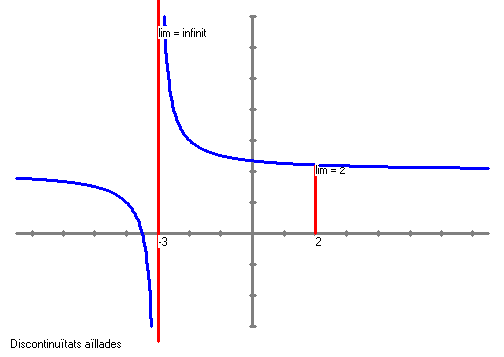
Una funció pot tenir tres tipus d'a´simptotes: verticals, horitzontals i oblíqües.

Una funció tindrà una asímptota vertical en un punt a si

Exemple té una asímptota vertical en x = 2 ja que

Quan tenim una funció que sigui un quocient de polinomis un criteri per trobar les asímptotes verticals és veure quins valors anul·len el denominador i mirar que el límit quan x tendeix a aquest números doni

Així per exemple la funció:

té dos punts que anul·len el denominador x = -3 i x = 2

Si calculem per la qual cosa hi ha una asímptota vertical en el punt x = -3 i si calculem per la qual cosa no hi ha una asímptota vertical en el punt x = -3. El que hi ha és una discontinuïtat evitable.

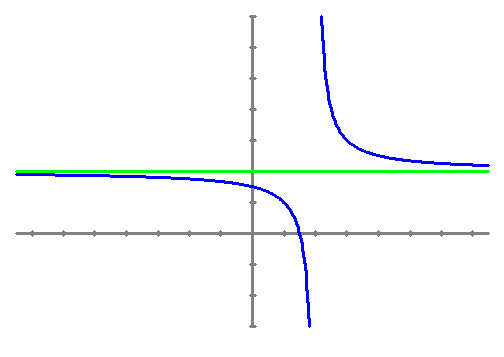
Una funció tindrà una asímptota horitzontal si

Exemple té una asímptota horitzontal la equació de la qual és y = 2 ja que

En aquest cas el lim quan f(x) tendeix a i quan tendeix a és el mateix, però en general cal calcular i ja que podria ser que les dues asímptotes no coincidissin o que en algun costat no n'hi hagués (o no n'hi hagués per cap costat.

La funció f(x) = e^x té només una asímptota horitzontal, quan i

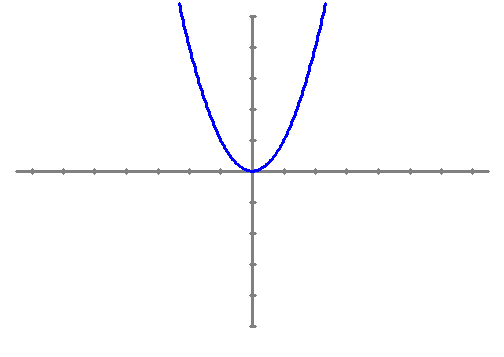
La funció f(x) = x² no té cap asímptota horitzontal ja que i

Una funció tindrà una asímptota oblíqua (en cas de que no les tingui horitzontals) si s'acosta a una recta y = mx + n.

Per exemple la funció s'acosta a la funció y = x + 2 quan x tendeix a i a

Per trobar les equacions de les asímptotes, en cas de que en tingui (cal fer els límits quan tendeix a i a ), s'ha de calcular els següents límits. En cas de què el primer límit no existeixi vol dir que la funció no té asímptotes oblíques:

Exemple: per calcular l'asímptota oblíqua de l'anterior funció hem de calcular:

Així l'equació de l'asímptota oblíqua queda: