(2024-juny-1-3) En Joan troba entre els papers del seu avi un esbós com el de la figura adjunta, on es descriu un terreny de regadiu que ha deixat en herència al seu pare. 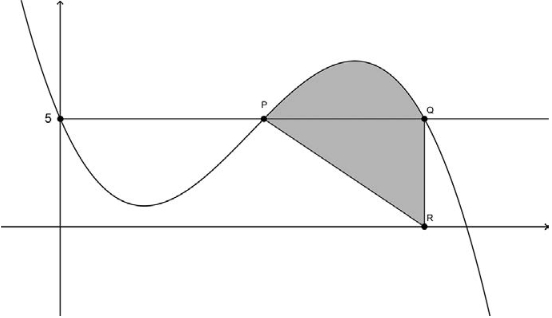La corba de la gràfica és `y = f(x)`, amb `f(x) = –x^3 + 7x^2 – 6x + 5`. a) A partir de l’expressió de `f(x)`, calculeu les coordenades dels punts `P`, `Q` i `R` indicats a la figura. Calculeu també l’equació de la recta `PR`. [1,25 punts] b) Calculeu la superfície del terreny. [1,25 punts] Solució: a) Per tobar els punts `P` i `Q` cal bcercar els valors de les `x` que facin que la funció sigui `5`. `–x^3 + 7x^2 – 6x + 5=5` `–x^3 + 7x^2 – 6x =0` `(–x^2 + 7x – 6)x =0` I això té una solució `x=0` que ja la sabíem, per la gràfica i: `–x^2 + 7x – 6=0` `x=(-7 pm\sqrt{7^2-4·(-1)·(-6)})/(2·(-1))=(-7pm\sqrt{25})/-2` `x_1=(-7+5)/-2=1` i `x_2=(-7-5)/-2=6` `P=(1,5)`, `Q=(6,5)` i `R=(6,0)` Per trobar l'equació de la recta que passa per `PR =>` que passa per `(1,5)` i `(6,0)`. Podem trobar el pendent `m=(0-5)/(6-1)=-5/5=-1` I per trobar l'equació amb aquesta pendent, `-1`, i que passa pel punt `(1,5)` `y-5=-1(x-1)` `y-5=-x+1` `y=-x+6` b) Per calcular l'area que ens demanen ho farem en dos trossos. 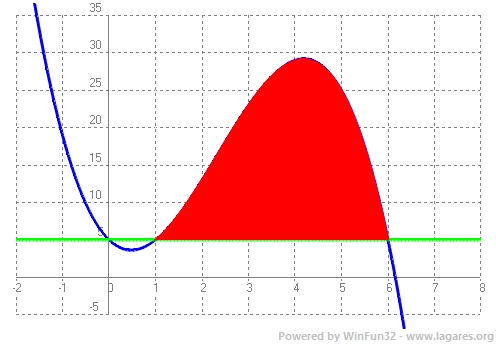1-L'àrea entre la funció i la recta `y=5` `\int_1^6 (–x^3 + 7x^2 – 6x + 5-5) dx` `\int_1^6 (–x^3 + 7x^2 – 6x ) dx` `[–x^4/4 + 7/3x^3 – 3x^2]_1^6` `(–(6^4)/4 + 7/3·6^3 – 3·6^2)-(–(1^4)/4 + 7/3·1^3 – 3·1^2)` `(–1296/4 + 7/3·216 – 3·36)-(–1/4 + 7/3 – 3)` `(-324+504-108)-(-0,25+2,333333-3) = 72,91666` 2-I l'àrea d'aquest triangle: 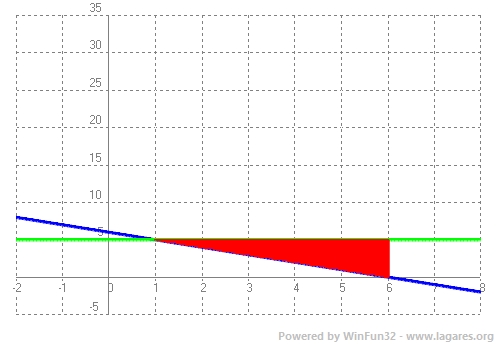`(5·5)/2=12,5` `u^2` Àrea total `= 72,91666+12,5 = 85,41666` `u^2`