|
Notes a les solucions:
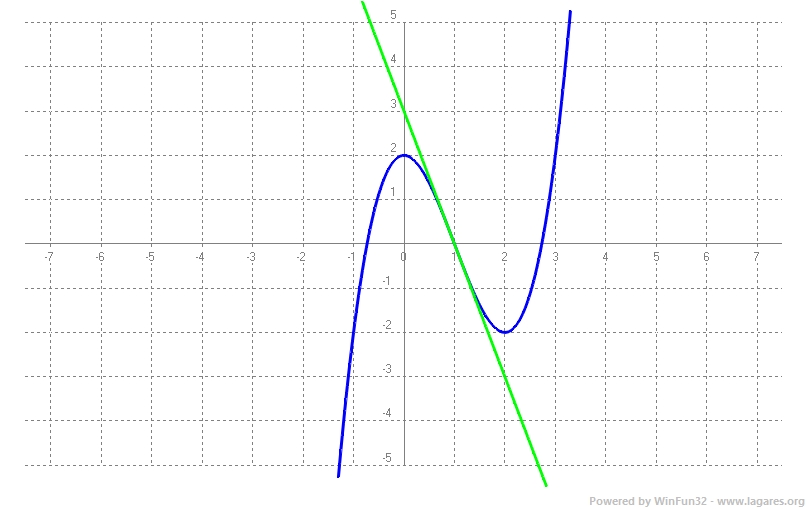
Qualsevol error, suggeriment o comentari podeu enviar-lo a jlagares@xtec.cat. 1-Calculeu els coeficients `a`, `b`, `c` i `d` de la funció `f(x) = ax^3 + bx^2 + cx + d` si sabem que l’equa- ció de la recta tangent a la gràfica de la funció `f` en el punt d’inflexió `(1, 0)` és `y = –3x + 3` i que la funció té un extrem relatiu en el punt de la gràfica d’abscissa `x = 0`. [2,5 punts] Solució:
Si en el punt d'inflexió, `(1,0)` la recta tangent és `y=-3x+3` vol dir que la derivada de `f(x)` en `x=1` val `-3 =>` Sí la funció té un extrem relatiu en el punt d'abscissa `x=0 =>` que la derivada en aquest punt val `0`. Tenim un sistema de `4` equacions amb `4` incògnites, de fet de `3` equacions amb `3` incògnites, ja que `c=0`. Si el podem resoldre tindrem la solució al nostre problema, el coeficients de la funció: $$ \begin{cases} a+b+d=0\\ 6a+2b=0\\ 3a+2b=-3 \end{cases} $$ I descobrim que encara és més senzill ja que les dues últimes equacions formen un sistema de `2` equacions amb `2` incògnites. El resoldrem i a partir de la primera equació podrem trobar la `d` que és la incògnita que ens faltarà. $$ \begin{cases} 6a+2b=0\\ 3a+2b=-3 \end{cases} $$ Fem una reducció multiplicant per `-2` la segona equació: $$ \begin{cases} 6a+2b=0\\ -6a-4b=6 \end{cases} $$ Ho sumem i ens queda: `-2b=6 => b=-3` Ho podem substituir a la primera equació Substituim `a=1` i `b=-3` a la primera equació `a+b+d=0 => 1-3+d=0 => d=2` Finalment queda la solució del problema `(a=1, b=-3, c=0, d=2)`: ANNEX:
 2-Considereu les dues matrius següents: $$ A=\begin{pmatrix} 2&-3&-5\\\ -1&4&5\\\ 1&-3&-4 \end{pmatrix} B=\begin{pmatrix} 2&2&0\\\ -1&-1&0\\\ 1&2&1 \end{pmatrix} $$ a) Calculeu les matrius `A · B` i `B · A`. [1,5 punts] Solució:
A·B=\begin{pmatrix} 2&-3&-5\\\ -1&4&5\\\ 1&-3&-4 \end{pmatrix} ·\begin{pmatrix} 2&2&0\\\ -1&-1&0\\\ 1&2&1 \end{pmatrix}= $$ $$ \begin{pmatrix} 2·2+(-3)·(-1)+(-5)·1&2·2+(-3)·(-1)+(-5)·2&2·0+(-3)·0+(-5)·1\\\ -1·2 + 4·(-1) + 5·1&-1·2 + 4·(-1) + 5·2&-1·0 + 4·0 + 5·1\\\ 1·2 + (-3)·(-1) + (-4)·1&1·2 + (-3)·(-1) + (-4)·2&1·0 + (-3)·0 + (-4)·1 \end{pmatrix}= $$ $$ \begin{pmatrix} 2&-3&-5\\\ -1&4&5\\\ 1&-3&-4 \end{pmatrix}=A $$ $$ B·A= \begin{pmatrix} 2&2&0\\\ -1&-1&0\\\ 1&2&1 \end{pmatrix}· \begin{pmatrix} 2&-3&-5\\\ -1&4&5\\\ 1&-3&-4 \end{pmatrix}= $$ $$ \begin{pmatrix} 2·2 +2·(-1) +0·1 &2·(-3) +2·4 +0·(-3) &2·(-5) +2·5 +0·(-4) \\\ (-1)·2 + (-1)·(-1) + 0·1 &(-1)·(-3) + (-1)·4 + 0·(-3) &(-1)·(-5) + (-1)·5 + 0·(-4) \\\ 1·2 + 2·(-1) + 1·1 &1·(-3) + 2·4 + 1·(-3) &1·(-5) + 2·5 + 1·(-4) \end{pmatrix}· $$ $$ \begin{pmatrix} 2 &2 &0 \\\ -1 &-1 &0 \\\ 1 &2 &1 \end{pmatrix}=B $$ b) Siguin `C` i `D` dues matrius quadrades del mateix ordre que satisfan `C · D = C` i `D · C = D`. Comproveu que les dues matrius, `C` i `D`, són idempotents. [1 punt] Nota: Una matriu quadrada s’anomena idempotent si coincideix amb el seu quadrat. Solució:
Multipliquem per `C` a cada costat
Com `D·C=D`, tenim:
I com hem partit de què `C·D=C` `=>`
Per la qual cosa `C` és idempotent per la definició que n'hem donat. 2-Tenim:
Multipliquem per `D` a cada costat
Com `C·D=C`, tenim:
I com hem partit de què `D·C=D` `=>`
Per la qual cosa `D` és idempotent per la definició que n'hem donat. ANNEX:
Ho podem comprovar amb la matriu `A`. Ha de passar que `A^2=A` $$ A^2=\begin{pmatrix} 2&-3&-5\\\ -1&4&5\\\ 1&-3&-4 \end{pmatrix}· \begin{pmatrix} 2&-3&-5\\\ -1&4&5\\\ 1&-3&-4 \end{pmatrix}= $$ $$ \begin{pmatrix} 2·2 +(-3)·(-1) + (-5)·1 &2·(-3) +(-3)·4 + (-5)·(-3) &2·(-5) +(-3)·5 + (-5)·(-4) \\\ (-1)·2 + 4·(-1) + 5·1 &(-1)·(-3) + 4·4 + 5·(-3) &(-1)·(-5) + 4·5 + 5·(-4) \\\ 1·2 +(-3)·(-1) +(-4)·1 &1·(-3) +(-3)·4 +(-4)·(-3) &1·(-5) +(-3)·5 +(-4)·(-4) \end{pmatrix}= $$ $$ \begin{pmatrix} 2 &-3 &-5 \\\ -1 &4 &5 \\\ 1 &-3 &-4 \end{pmatrix}=A $$ 3-Sigui la funció derivada d’una funció derivable` f(x)` que passa pel punt `A = (0, 3)`. $$ f'(x)=\begin{cases} x-1 \text{, si } x\le2\\ \\ \frac{1}{x-1} \text{, si } x>2\end{cases} $$ a) Calculeu la funció `f(x)`. [1,5 punts] Solució:
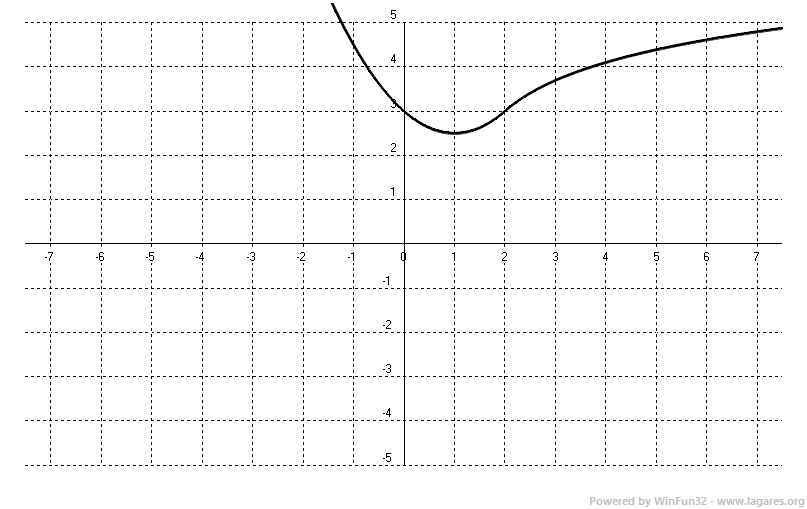
Com passa per `(0,3)` i `0 <=2 =>` que per calcular `f(0)` cal fer servir la primera funció i ens peremtrà trobar el valor de `C`. `f(0)=0^2/2-0+C=3 => C=3` Amb això tenim la funció definida: $$ f(x)=\begin{cases} \frac{x^2}{2}-x+3 \text{, si } x\le2\\ \\ ln(x-1)+C' \text{, si } x>2\end{cases} $$ Per trobar `C'` farem servir que la funció cal que sigui contínua en `x=2` (ja que ens han dit que és derivable) per la qual cosa cal que calculem el límit per la dreta i el límit per l'esquerra quan tendim a `2` i fer que siguin iguals. `\lim_{x\to 2^-} [x^2/2-x+3] =\lim_{x\to 2^+} [ln(x-1)+C'] =>` `2^2/2-2+3 = ln(2-1)+C' =>` `2-2+3 =ln(1)+C' =>` `3 =0+C' => C' = 3` Amb tot això tenim que la funció és: $$ f(x)=\begin{cases} \frac{x^2}{2}-x+3 \text{, si } x\le2\\ \\ ln(x-1)+3 \text{, si } x>2\end{cases} $$ ANNEX:
 b-Calculeu l’equació de la recta tangent a la funció `f'(x)` en el punt d’abscissa `x = 3`. [1 punt] Solució:
I el que ens demanen és l'equació d ela recta tangent de `f'(x)` o sigui cal calcular `f''(x)= (-1)/(x-1)^2` Per trobar l'equació de la recta tangent, cal un punt `f'(3)=1/(3-1)=1/2 => (3,1/2)` i el pendent: `f''(3)=(-1)/(3-1)^2=(-1)/4` Per trobar l'equació de la recta tangent podem fer servir, per exemple, l'equació punt-pendent: Que en el nostre cas és: Si volem l'equació explícita: 4-Sigui el sistema d’equacions lineals següent, que depèn del paràmetre real `\lambda`: $$ \begin{cases} x+2\lambda y+(2+\lambda)z=0\\ (2+\lambda)x+y+2\lambda z=3\\ 2\lambda x+(2+\lambda)y+z=-3\end{cases} $$ a) Discutiu el sistema per als diferents valors del paràmetre `\lambda`. [1,25 punts] Solució:
$$ \begin{vmatrix} 1&2\lambda&2+\lambda\\\ 2+\lambda&1&2\lambda\\\ 2\lambda&2+\lambda&1 \end{vmatrix}= $$
| 1 0 0 1
|
-1 | -1 1 -1
-----+------------------------
1 -1 1 0
L'equació de segon grau no té cap arrel real ja que el discriminant és negatiu: O sigui l'única solució és `lambda=-1` El que implica si `lambda \ne -1` Determinant de la matriu del sistema `\ne 0 =>` Rang matriu sistema `=3` Rag ampliada `=3` ja que tenim `3` files `=>` Si `lambda=-1` Determinat matriu del sistema `=0` Rang matriu del sistema `<2` Anem a calcular el determinat d'un menor de la matriu ampliada, dues primeres columnes i termes independents (recordem `lambda=-1`). Agafem la primera matriu d'ordre dos: $$ \begin{vmatrix} 1&-2\\\ 1&1 \end{vmatrix}=1+2=3\ne0 => $$ Rang matriu del sistema `=2`. Orlem amb la única matriu `3x3` de la matriu ampliada i calculem el determinant. $$ \begin{vmatrix} 1&-2&0\\\ 1&1&3\\\ -2&1&-3 \end{vmatrix}=-3+12+0-(0+3+6)=0 => $$ Rang matriu ampliada no és `3 =>` Rang matriu ampliada és `2 =>` com els rang son iguals i més petits que el número d'incògnites. b-Per al cas `\lambda = –1`, resoleu el sistema, interpreteu-lo geomètricament i identifiqueu-ne la solució. [1,25 punts] Solució:
\begin{cases} x-2y+z=0\\ x+y-2z=3\\ -2x+y+z=-3\end{cases} $$ Fem Gauss. A la 1a 2a li resto la primera i a la 3a li sumo 2 vegades la primera $$ \begin{cases} x-2y+z=0\\ 3y-3z=3\\ -3y+3z=-3\end{cases} $$ A la tercera li sumo la segona $$ \begin{cases} x-2y+z=0\\ 3y-3z=3\\ 0=0\end{cases} $$ O sigui és un sitema compatible indeterminat, ja que ens han quedat dues equacions, linealment independents, el rang de la matriu del sistema val `2` ja que: $$ \begin{vmatrix} 1&-2\\\ 0&3 \end{vmatrix}=3 $$ Diferent de `0` i com que hi ha dues equacons el rang de l'ampliada no pot ser més gran que `2`. `Rang A = Rang A' <` número d'incògnites. Sistema compatible indeterminat. El que ens queda és $$ \begin{cases} x-2y+z=0\\ 3y-3z=3\end{cases} $$ Que és l'equació d'una recta. L'interpretació geomètrica del sistema és: Tres plans que es tallen en una recta. Si el que volem com a solució és l'equació vectorial podem segir fent Gauss. $$ \begin{cases} x-2y+z=0\\ 3y-3z=3\\ z=\lambda\end{cases} $$ $$ \begin{cases} x-2y+\lambda=0\\ 3y-3\lambda=3\\ z=\lambda\end{cases} $$ $$ \begin{cases} x-2y=-\lambda\\ 3y=3+3\lambda\\ z=\lambda\end{cases} $$ $$ \begin{cases} x-2y=-\lambda\\ y=1+\lambda\\ z=\lambda\end{cases} $$ $$ \begin{cases} x-2(1+\lambda)=-\lambda\\ y=1+\lambda\\ z=\lambda\end{cases} $$ $$ \begin{cases} x=2+\lambda\\ y=1+\lambda\\ z=0+\lambda\end{cases} $$ I ho podem posar com equació vectorial: `(2,1,0)` vector de posició i `(1,1,1)` vector director. 5-La Núria té un jardí rectangular i vol fer-hi un tan-cat (rectangular o quadrat) de `8` `m^2` per al seu gos. Ha pensat de posar el tancat tocant al mur del jardí, tal com es mostra a la figura de la dreta, per estalviar-se així un dels quatre costats. El preu de la tanca que vol fer servir és de `2,5` €/m.  a)Quines dimensions ha de tenir el tancat perquè el cost sigui mínim? Quin és aquest cost mínim? [1,75 punts] Solució: 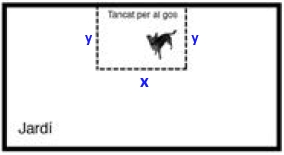 Si en diem `x` a la part de la tanca horitzontal i `y` a la vertical la funció a optimitzar, preu és el perímetre per `2,5` €/m. Tenint en compte que la part superior no hi ha tanca, ja que hi ha el mur, el perímetre és `2y+x` per la qual cosa la funció a optimitzar, preu és: Però com la superfície ha de ser de `8` `m^2` tenim un lligam entre `x` i `y` que és que `x·y=8` (que és l'àrea. `=> y=8/x` la qual cosa fa que la funció a optimitzar sigui: Com volem que aquest preu sigui mínim, cal trobar-lo. Calculem els punts on la derivada sigui `0` i comprovarem que realment es tracta d'un mínim. `2,5-40/x^2=0` `2,5=40/x^2` `x^2=40/(2,5)` `x^2=16 => x=\sqrt{16}=+-4` La solució negativa no teé massa sentit i ens centrarem en la positiva `x=4`, cal demostrar que es un mínim. Calcularem la segona derivada i mirarem que dona positiu. Que si substituim per `x=4 => p''(4)=80/4^3>0 =>` que a `x=4, p(x)` té un mínim. Acabem l'exercici si `x=4 => y=8/x => y=8/2=2` per la qual cosa les dimensions de la tanca son: Cal comprar `8` metres de tanca ja que hi ha dues altures i una base i el preu `p=2,5*8 = 20` €. b)Si manteniu la forma rectangular o quadrada del tancat i feu que un dels vèrtexs del jardí coincideixi amb un vèrtex del tancat, quants euros us podeu estalviar? Raoneu com posaríeu el tancat i justifiqueu amb càlculs matemàtics les dimensions de la vos-tra proposta. [0,75 punts] Solució: 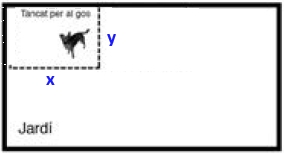
Si calculem la derivada i la igualem a `0`. Com abans només tenim en compte la solució positiva. Calculem la segona derivada per comprovar que és un mínim: Que si ho substituim per un nombre positiu, `p''(\sqrt{8})=20/(\sqrt{8}^3) >=0`. O sigui a `x=\sqrt{8}` hi ha un mínim. I la dimensió `y=8/\sqrt{8}=\sqrt{8}` que resulta que `x` i `y` son iguals el que resulta és que la tanca formarà un quadrat. El cost: Obtindriem un estalvi de `20-14,14 = 5,86` €. 6-Siguin els plans `pi_1` i `pi_2`, determinats respectivament per les equacions `pi_1: x + y = 3` i `pi_2: x – z = –2`. a)Trobeu l’equació general `(Ax + By + Cz + D = 0)` del pla `pi_3`, que és perpendicular a `pi_1` i `pi_2`, i que passa pel punt `P = (4, 1, 2)`. [0,75 punts] Solució:
$$ \begin{vmatrix} i&j&k\\\ 1&1&0\\\ 1&0&-1 \end{vmatrix}=-1i+-(-1)j-1k= -i+j-k $$ El vector associat al pla `pi_3 = (-1,1,-1)` Si en el producte vectorial haguéssim posat els vectors al revés ens ves donat el mateix vector canviat de signe, que, també és un bon vector associat. Així la nostra equació del pla és: Com passa pel punt `P =>` Per la qual cosa l'equació del pla cercat és: ANNEX:
$$ \begin{vmatrix} x-4&y-1&z-2\\\ 1&1&0\\\ 1&0&-1 \end{vmatrix}=0 $$ b)Sigui `r` la recta d’intersecció de `pi_1` i `pi_2`. Calculeu l’equació vectorial de la recta `r`. [0,75 punts] Solució:
$$ \begin{cases} x + y = 3\\ x – z = –2\\ z=\lambda \end{cases} $$ $$ \begin{cases} x + y = 3\\ x – \lambda = –2\\ z=\lambda \end{cases} $$ $$ \begin{cases} x + y = 3\\ x = –2+\lambda\\ z=\lambda \end{cases} $$ A la primera equació substituim `x` pel seu valor en funció de `lambda` i tenim, `-2+lambda+y=3 => y=5-lamda` $$ \begin{cases} x = –2+\lambda\\ y=5-\lambda\\ z=\lambda \end{cases} $$ I ens queda: ANNEX:
Es pot comprovar que aquest vector de posició pertany als dos plans, per la qual cosa a la seva intersecció, ho sigui a la recta que defineixen. \begin{cases} x + y = 3\\ x – z = –2 \end{cases} $$ $$ \begin{cases} -2 + 5 = 3\\ -2 – 0 = –2 \end{cases} $$ c)Calculeu el punt `Q` de la recta `r` que és més a prop del punt `P`. [1 punt] Solució:
I com tenim que l'equació de la recta és: Ho sbstituim a l'equació del pla: Ho substituim a l'equació de la recta: |