|
Fórmules d'addició: 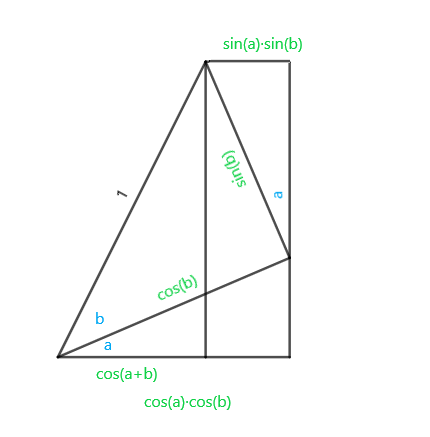 Del dibuix es dedueix:
I a partir d'aquí es poden deduir fàcilment totes les altres: Per fer-ho, cal recordar i fer servir:
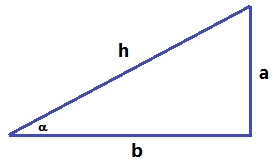 `sin(\alpha)=a/h` i `cos(\alpha)=b/h` `a^2+b^2=h^2 => a^2/h^2+b^2/h^2=h^2/h^2 =>` `a^2/h^2+b^2/h^2=1 => sin^2(\alpha)+cos^2(\alpha)=1` 2- `sin(-a) = -sin(a)` i 3- `cos(-a) = cos(a)` 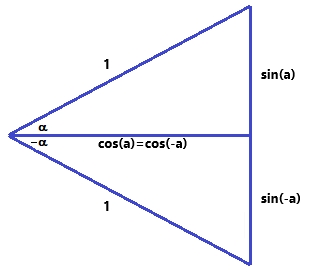 4- `sin(90-a) = cos(a)` 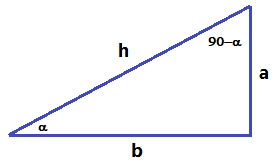 5-`cos(90-a) = sin(a)` 6- `tan(-a)=``sin(-a)/cos(-b)=-sin(a)/cos(b)``=-tan(a)` 1- `cos(a-b) = cos(a)·cos(b)+sin(a)·sin(b)` Demostració:
`cos(a)·cos(b)-sin(a)·[-sin(b)]=cos(a)·cos(b)+sin(a)sin(b)` 2- `sin(a+b) = sin(a)·cos(b)+cos(a)·sin(b)` Demostració:
`cos(90-a)·cos(b)+sin(90-a)·sin(b)=sin(a)·cos(b)+cos(a)·sin(b)` 3- `sin(a-b) = sin(a)·cos(b)-cos(a)·sin(b)` Demostració:
`sin(a)cos(b)+cos(a)·[-sin(b)]=sin(a)cos(b)-cos(a)·sin(b)` 4- `tan(a+b) = (tan(a)+tan(b))/(1-tan(a)·tan(b))` Demostració:
`((sin(a)cos(b))/(cos(a)cos(b))+(cos(a)sin(b))/(cos(a)cos(b)))/((cos(a)cos(b))/(cos(a)cos(b))-(sin(a)sin(b))/(cos(a)cos(b)))=(tan(a)+tan(b))/(1-tan(a)tan(b))` 5- `tan(a-b) = (tan(a)-tan(b))/(1+tan(a)·tan(b))` Demostració:
`(tan(a)-tan(b))/(1-tan(a)·[-tan(b)])=(tan(a)-tan(b))/(1+tan(a)·tan(b))` Angle doble: 1- `cos(2a) = cos^2(a)-sin^2(a)` Demostració:
2- `sin(2a) = 2sin(a)·cos(a)` Demostració:
3- `tan(2a) = (2tan(a))/(1-tan^2(a))` Demostració:
Angle meitat: 1 - `cos(a/2) = \pm sqrt((1+cos(a))/2)` Demostració:
`cos(a) = cos^2(a/2)-sin^2(a/2) =cos^2(a/2)-[1-cos^2(a/2)] = -1+2cos^2(a/2)` `cos(a) = -1+2cos^2(a/2)` `1+cos(a) = 2cos^2(a/2)` `(1+cos(a))/2 = cos^2(a/2)` `cos(a/2)= pm \sqrt{(1+cos(a))/2}` 2 - `sin(a/2) = \pm sqrt((1-cos(a))/2)` Demostració:
`cos(a) = cos^2(a/2)-sin^2(a/2) =1-sin^2(a/2)-sin^2(a/2) = 1-2sin^2(a/2)` `cos(a) = 1-2sin^2(a/2)` `2sin^2(a/2) = 1-cos(a)` `sin(a/2) = pm \sqrt{(1-cos(a))/2}` 3 - `tan(a/2) = \pm sqrt((1-cos(a))/(1+cos(a))` Demostració:
Transformació de sumes en productes: 1 - `sin(A) + sin(B) = 2cos((A-B)/2)· sin((A+B)/2)` Demostració:
`2a = A+B => a=(A+B)/2` `2b = A-B => b=(A-B)/2` `sin(A)+sin(b)= sin(a+b)+sin(a-b)=` `sin(a)cos(b)+cos(a)sin(b)+sin(a)cos(b)-cos(a)sin(b) = 2sin(a)cos(b)=` `2sin((A+B)/2)·cos((A-B)/2)` 2 - `sin(A) - sin(B) = 2sin((A-B)/2) · cos((A+B)/2)` Demostració:
`sin(a)cos(b)+cos(a)sin(b)-sin(a)cos(b)+cos(a)sin(b) = 2cos(a)sin(b)=` `2cos((A+B)/2)·sin((A-B)/2)` 3 - `cos(A) - cos(B) = -2sin((A-B)/2)· sin((A+B)/2)` Demostració:
`cos(a)cos(b)-sin(a)sin(b)-cos(a)cos(b)-sin(a)sin(b)=-2sin(a)sin(b)` `-2sin((A+B)/2)·sin((A-B)/2)` 4 - `cos(A) + cos(B) = 2cos((A-B)/2)· cos((A+B)/2)` Demostració:
`cos(a)cos(b)-sin(a)sin(b)+cos(a)cos(b)+sin(a)sin(b)=2cos(a)cos(b)` `2cos((A+B)/2)·cos((A-B)/2)=` Exemple: `A =444` i `B = 436` `cos(444) + cos(436) = 2cos((444-436)/2)· cos((444+436)/2)` `cos(444) + cos(436) = 2cos(4)· cos(444)` I aixň suposa alguna cosa:
|