|
Anem a estudiar un altre concepte de les funcions, el de continuïtat d'una funció en un punt. Va molt lligat al que acabem d'estudiar sobre els límits. Per ajudar a entendre'l veurem uns gràfics. 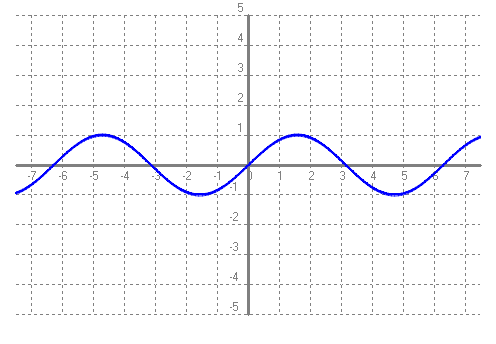 Ara mira el dibuix de la funció del primer exercici de límits: 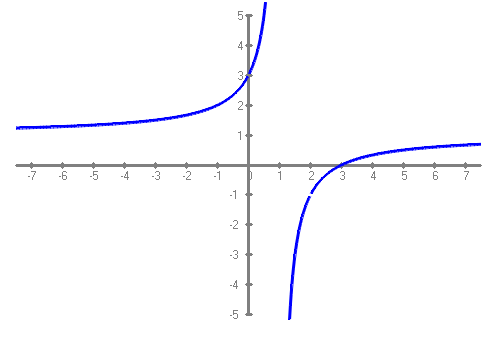 Suposo que hi veureu una gran diferència. `f(x)=sin(x)` és contínua sempre. En canvi, `f(x)=(x^3-5x^2+6x)/(x^3-3x^2+2x)`, té uns quants punts de discontinuïtat. `x=0` (evitable), `x=1` (asimptòtica), `x=2` (evitable) N'hi ha d'un altre tipus, es diu, discontinuïtat de salt: 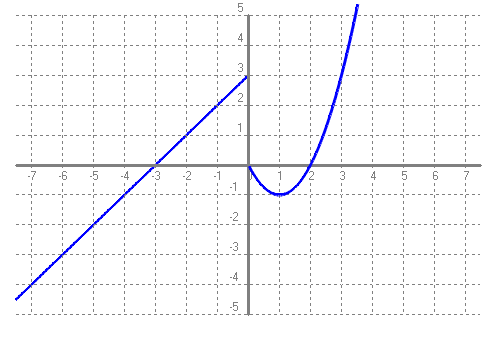 Anem a estudiar aquestes discontinuïtats de forma independent. 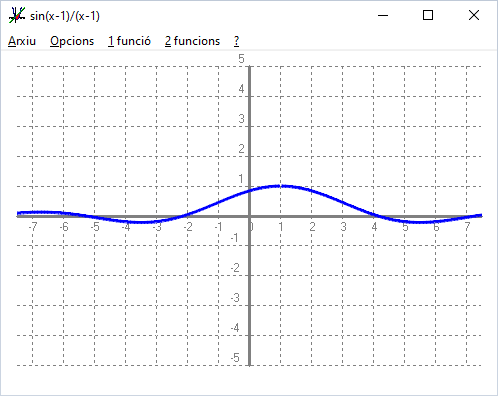
Però tots veieu clar que si calculem el `lim_{x\to 0} sin(x-1)/(x-1)=1` per la qual cosa si definíssim `f(1)=1` la funció deixaria de ser discontínua. Com hem pogut donar un valor a `f(1)` de manera que la funció deixi de ser discontínua direm que quan ens trobem amb aquest tipus de discontinuitat en direm, discontinuïtat evitable. 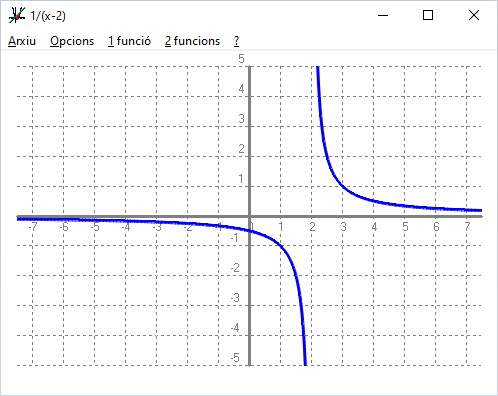
Però tots veieu clar que si calculem el `lim_{x\to 2^-} 1/(x-2)=+\infty` i `lim_{x\to 2^+} 1/(x-2)=-\infty`. En general quan en un punt el `lim_{x\to a} f(x)=\infty` diem que a `x=a` i ha una asímptota vertical i, `x=a` és la seva equació. Per la qual cosa quan ens trobem amb aquest tipus de discontinuïtat en direm, discontinuïtat asimptòtica. 
Però tots veieu clar que si calculem el `lim_{x\to 0^-} f(x)=3` i `lim_{x\to 0^+} f(x)=0`. En general quan en un punt el `lim_{x\to a^-} f(x) \neq lim_{x\to a^+} f(x)` ens trobem amb un altre tipus de discontinuïtat que en diem discontinuïtat de salt. Aquest tipus de discontinuïtat ens el trobarem amb les funcions definides a trossos en la frontera dels trossos. Per cert no sempre hi ha una discontinuïtat en una frontera d'una funció definida a trossos. Per tot el que acabam de veure. Una funció no és continua en un punt si no està definida en aquest punt i tampoc ho és si els límits per la dreta i l'esquerra són diferents. Definirem funció contínua en un punt si es compleixen les següents condicions: `f(x)` és contínua en un punt `a <=>`
2-Existeixi `lim_{x\to a} f(x)` això implica que existeixin els límits per l'esquerra i la dreta i siguin iguals. `lim_{x\to a^-} f(x)=lim_{x\to a^+} f(x)` 3-Que les dues coses siguin iguals, `lim_{x\to a} f(x)=f(a)` Evidentment quan en un punt,`lim_{x\to a} f(x)=\infty` la funció és discontínua (discontinuïtat asimptòtica). Exemple: Estudia la continuïtat de la funció:  Hem de mirar si es dicontínua en algun punt. Com és una funció definida a trossos hem de mirar els punts de discontinuïtat per `x<=0` fent servir la funció, `(x^2-1)/(x^2+2x+1)`. Llavors buscar els punts de discontinüitat per `x>0` fent servir al funció `2x^2-1`. I finalment veure què passa en la frontera, o sigui a `x=0`, per la qual cosa caldrà calcular els límits per cada costat, veure si n'hi ha si coincidexien i si coincideixen amb la imatge de `f(0)`. 1-Continuïtat per `x<=0`.
Com és un quocient hem de mirar on val `0` i on passi la funció o estarà definida, per la qual cosa serà discontínua. `x^2+2x+1=0 => x=-1` Com que és del tros `x<=0`, `f(x)` no està definida en `x=-1`, o sigui segur que és discontínua en `x=-1`. Pels altres nombres `x<=0` la funció és contínua. Hem de mirar el tipus de discontinuïtat. `lim_{x\to -1}((x-1)·(x+1))/((x+1)^2)=lim_{x\to -1}(x-1)/(x+1)=(-2)/0=\infty`. Això vol dir que a `x=-1` hi ha una discontinuïtat asimptòtica
3-Continuïtat a la frontera, `x=0`.
`lim_{x\to 0^-}f(x)=lim_{x\to 0^-}(x^2-1)/(x^2+2x+1)=(-1)/1=-1` `lim_{x\to 0^+}f(x)=lim_{x\to 0^+}2x^2-1=-1` Com que els dos límits són iguals podem dir sense cap problema que: `lim_{x\to 0}f(x)=-1` Per trobar `f(0)` cal fer servir la funció, `(x^2-1)/(x^2+2x+1)`, ja que `x=0<=0`. `f(0)=(0^2-1)/(0^2+2·0+1)=(-1)/1=-1` `lim_{x\to 0}f(x)=-1=f(0=`. Per la qual cosa `f(x)` és contínua en `x=0`. Resultat final: `f(x)` és contínua `R-{-1}`. I a `x=-1` hi ha una discontinuïtat asimptòtica. 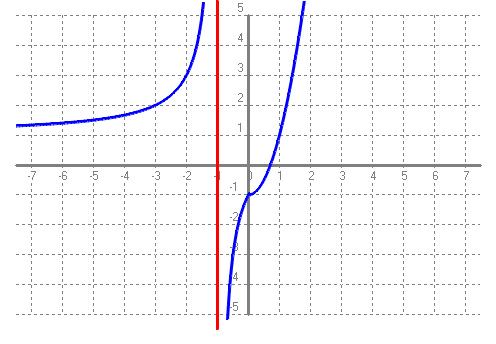 A continuació el que cal és fer exercicis al respecte:
Solució 9 a Solució 9 b Solució 10 Solució 11 Solució 12 |