|
És el lloc geomètric dels punts del pla tals que la distància a un punt anomenat focus és igual a la distància a una recta que anomenarem directriu de la paràbola.. 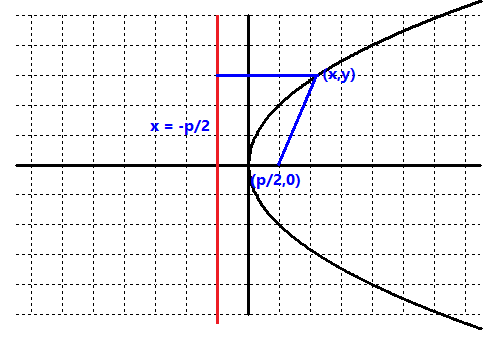 Coordenada del focus `= (p/2,0)` Equació de la directriu` x=-p/2 ` La distància de `(p/2,0)` a `(x,y)= sqrt((x-p/2)^2+y^2)` La distància de `x=-p/2` a `(x,y)= x+p/2` `x+p/2=sqrt((x-p/2)^2+y^2)` Ho elevem tot al quadrat. `(x+p/2)^2=(x-p/2)^2+y^2` `x^2+2p/2x+(p/2)^2=x^2-2xp/2+(p/2)^2+y^2` `x^2+2p/2x+(p/2)^2=x^2-2xp/2+(p/2)^2+y^2` `2p/2x=-2xp/2+y^2` `2px=y^2` |