|
És el lloc geomètric dels punts del pla tals que la suma de les seves distàncies a dos punts fixos anomenats focus, és constant. Aquesta constant en direm `2a`. 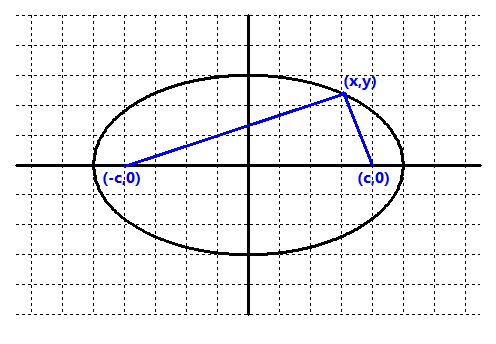 La suma de les distàncies `= 2a` La distància de `(c,0)` a `(x,y)= sqrt((x-c)^2+y^2)` La distància de `(-c,0)` a `(x,y)= sqrt((x+c)^2+y^2)` Aïllem una arrel quadrada, de manera que no ens quedi una suma d'arrels quadrades quan ho elevem tot al quadrat. `sqrt((x-c)^2+y^2)=2a-sqrt((x+c)^2+y^2)` Tot elevat al quadrat `(x-c)^2+y^2=4a^2-2·2a·sqrt((x+c)^2+y^2)+(x+c)^2+y^2` `x^2-2cx+c^2+y^2=4a^2-4a·sqrt((x+c)^2+y^2)+x^2+2cx+c^2+y^2` Treiem el que és igual a cada costat de l'equació. `-2cx=4a^2-4a·sqrt((x+c)^2+y^2)+2cx` Deixem sola l'arrel en un costat. `4a·sqrt((x+c)^2+y^2)=4a^2+4cx` `sqrt((x+c)^2+y^2)=a+(cx)/a` Ho elevem tot al quadrat. `(x+c)^2+y^2=(a+(cx)/a)^2` `x^2+2cx+c^2+y^2=a^2+2cx+((cx)/a)^2` `x^2+c^2+y^2=a^2+(c^2x^2)/a^2` `x^2-(c^2x^2)/a^2+y^2=a^2-c^2` `(1-c^2/a^2)x^2+y^2=a^2-c^2` `((a^2-c^2)/a^2)x^2+y^2=a^2-c^2` Ho dividim tot per `a^2-c^2` `x^2/a^2+y^2/(a^2-c^2)=1` 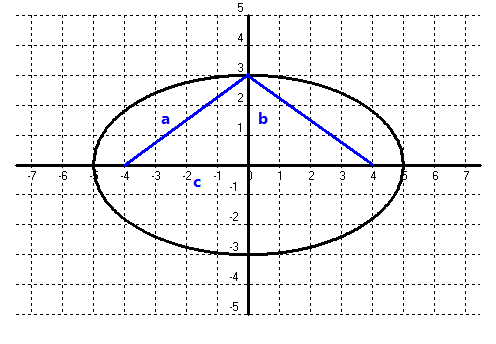 Si mirem el dibuix veiem que `c`, `b`, i `a` són les tres costats d'un triangle rectangle que compleixen el teorema de Pitàgores, `a^2-c^2=b^2` i l'equació queda: Que és l'equació de l'el·lipse centrada a l'origen de coordenades. Fixeu-vos que `(-a,0)` i `(a,0)` són el punts de tall en l'eix `x`, `a` s'en diu semieix horitzontal. I `(-b,0)` i `(b,0)` són el punts de tall en l'eix `y`, s'en diu semieix vertical. |