Matemàtiques - 1r BAT - Còniques. Exercicis Final 19.



19-Troba els valors que ha de tenir m tal que la recta `y=x+m` sigui tangent a l'el·lipse d'equació `x^2+2y^2=6`.


SOLUCIÓ:

    Perquè la recta sigui tangent a l'el·lipse si busquem els punts de tall (resoldre el sistema) només ha de tenir una solució.


      `y=x+m` i `x^2+2y^2=6`, fem una substitució.


      `x^2+2(x+m)^2=6`


      `x^2+2(x^2+2mx+m^2)=6`


      `x^2+2x^2+4mx+2m^2=6`


      `3x^2+4mx+2m^2-6=0`


      `x=(-4m\pm sqrt((4m)^2-4·3·(2m^2-6)))/6`


    Perquè només tingui una solució el discriminant (el que hi ha dins l'arrel) ha de ser `0`.


      `(4m)^2-4·3·(2m^2-6)=0`


      `(4m)^2-12·(2m^2-6)=0`


      `16m^2-24m^2+72=0`


      `-8m^2+72=0`


      `m^2=(-72)/(-8)=9`


    `m=\pm sqrt(9) = \pm3`


    O sigui les rectes són `y=x+3` i `y=x-3`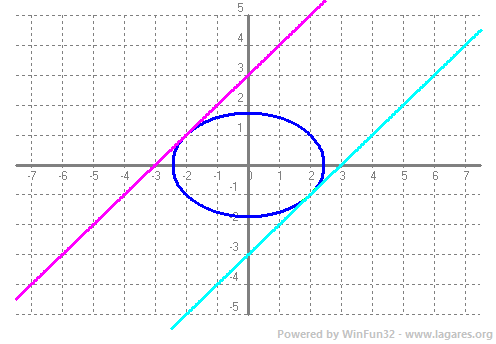