Matemàtiques - 1r BAT - Còniques. Exercicis Final 17. 17-Determina l'equació de a recta tangent a la circumferència `x^2+y^2+3x-2y-3=0` que passa pel punt `(0,-1)`. SOLUCIÓ: Si substitueixo el punt `(0,-1)` en la circumferència `x^2+y^2+3x-2y-3=0` descobreixo que `0^2+(-1)^2+3·0-2·(-1)-3=1+2-3=0` la qual cosa vol dir que el punt és de la circumferència. Ara busquem el centre de la circumferència `a=-3/2` i `b=2/2=1 => (-3/2,1)`. cal calcular el vector que va del punt al centre `(-3/2,1)-(0,-1)=(-3/2,2)` això és un vector perpendicular a la recta tangent cercada, o sigui l'associat. `-3/2x+2y+c=0` Substituïm al punt `(0,-1) => -3/2·0+2·(-1)+c=0 => c=2` Finalment l'equació de la recta buscada és: 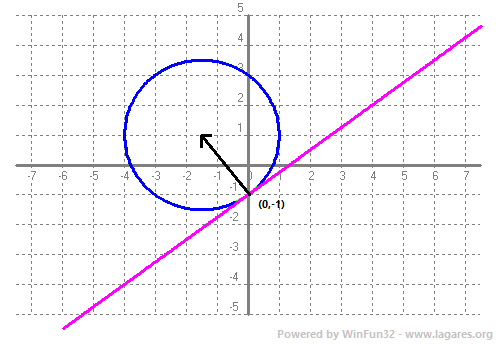`-3/2x+2y+2=0` i en la forma explícita `y=3/4x-1`