Matemàtiques - 1r BAT - Còniques. Exercicis Final 16. 16-Calcula `k` de manera que la recta `3x+y+k=0` sigui tangent a la circumferčncia `x^2+y^2-6x=0`. SOLUCIÓ: Calculem el radi i el centre de la circumferčncia: `a=-3` i `b=0` i `r=3` La forma més fŕcil de resoldre la pregunta és demanar que la distŕncia de la recta al centre `(3,0)` sigui igual que el radi `3`. `d=(|3x+y+k|)/sqrt(3^2+1^2)=(|3x+y+k|)/sqrt(10)` `3=(|3·3+0+k|)/sqrt(10)=(9+k)/sqrt(10)` `3sqrt(10)=9+k` `9·10=(9+k)^2=81+18k+k^2` `90=81+18k+k^2` `k^2+18k-9=0` `k_1=-9+3sqrt(10)` i `k_2=-9-3sqrt(10)` Hi ha dues rectes paral·leles: 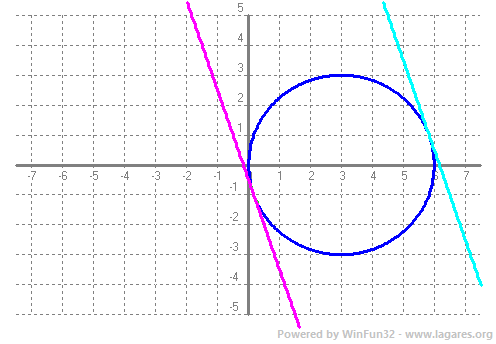`3x+y-9+3sqrt(10)=0` i `3x+y-9-3sqrt(10)=0`