|
15-Contesta les preguntes següents a partir de les dues circunferències, C': la de centre `(3,7)` i que passa pel punt `(-2,7)` i la d'equació C:`x^2+y^2+4x-10y+20=0`. a-Quina és la posició relativa entre elles? SOLUCIÓ:
A C' necessitem trobar el radi que és la distància entre els dos punts, `(3,7)-(-2,7)=(5,0)` i ara cal calcular el mòdul, `r=sqrt(5^2+0^2)=5` Per la qual cosa l'equació de C', `x^2+y^2-2·3-2·7+3^2+7^2-5^2 =0 => x^2+y^2-6x-14y+33=0` Per trobar la posició relativa cal que resolem el sistema: `x^2+y^2+4x-10y+20=0` `x^2+y^2-6x-14y+33=0` Restant les dues equacions: `10x+4y-13=0 => y = (13-10x)/4` i ho substituïm a una de les equacions: `x^2+((13-10x)/4)^2-6x-14·(13-10x)/4+33=0` Si ho arreglem l'equació queda: `116x^2+204x-31=0` i les solucions són: `x_1=-51/58-(5sqrt(35))/29 \approx -1'9` i `y_1=(13-10·(-1,9))/4 \approx 8` `x_2=-51/58+(5sqrt(35))/29 \approx 0'14` i `y_2=(13-10·(0'14))/4 \approx 2'9` Tenim dues circumferències secants ja que es tallen en dos punts, `(-1'9,8)` i `(0'14,2'9)` 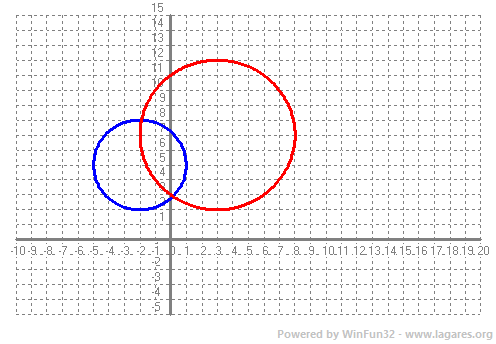 Recordem que aquest problema es podia fer d'una altra manera. Es podia calcular la distancia entre els dos centres i veure que era menor que la suma dels dos radis, per la qual cosa les dues circumferències es tallen. Això és molt més senzill i infinitament més curt, però com que més endavant necessitem calcular aquests punts d'intersecció, ja tenim la feina feta :-) b-Calcula l'eix radical. SOLUCIÓ:
Hem d'igualar les dues equacions i l'equació que queda és l'equació de (la recta) eix radical. `x^2+y^2+4x-10y+20=x^2+y^2-6x-14y+33` 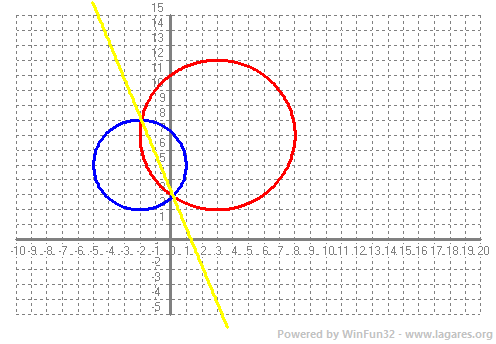 c-Calcula la intersecció de la cicumferència C amb l'eix radical. explica el que hi observes. 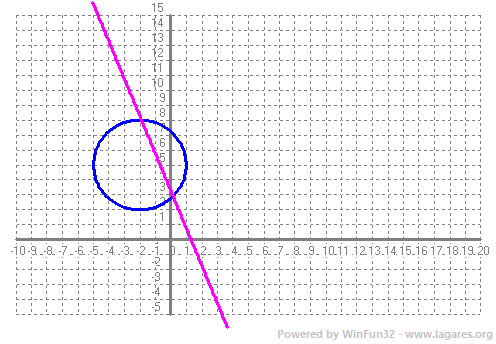 SOLUCIÓ:
Recordem que els nombres són aproximats. d-Quina és la longitud de la corda que determina C' amb l'eix radical? 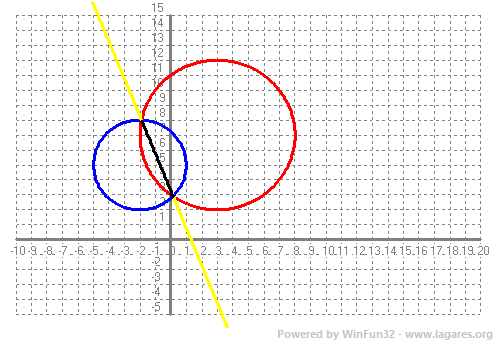 SOLUCIÓ:
la longitud de la corda és la distància entre els dos punts anteriors, `(-1'9,8)` i `(0'14,2'9)`. Cal calcular el mòdul del vector que va de l'un a l'altre, `(-1'9,8)-(0'14,2'9)= (-2'04,5'1)` |