Matemàtiques - 1r BAT - Còniques. Exercicis Final 08.



8-Calcula les equacions de les tangents a la circumferència `x^2+y^2-6x-4y+4=0` en els punts de tall amb els eixos.


SOLUCIÓ:

    `x^2+y^2-6x-4y+4=0` centre `= (3,2)`, radi `3^2+2^2-r^2=4 => r=3`


    Punts de tall eix `y`:

    `x=0` | `x^2+y^2-6x-4y+4=0 => y^2-4y+4=0 => y=2 => (0,2)`


    Vector que va del centre `(3,2)` a `(0,2)`, `(3,2)-(0,2)=(3,0)` que és l'associat de la nostra recta. Equació `3x+0y+c=0 => 3x+c=0`

    Com passa pel punt `(0,2) => 3·0+0·2+c=0 => c=0 => 3x+0y+0=0 => 3x=0`. L'equació de la recta queda:


    `x=0`




    Punts de tall eix `x`:

    `y=0` | `x^2+y^2-6x-4y+4=0 => x^2-6x+4=0 =>`

    `x_1=3-sqrt(5) => (3-sqrt(5),0)`

    `x_2=3+sqrt(5) => (3+sqrt(5),0)`


    Busquem els vectors de cadascun d'aquests punts al centre:

    `(3,2)-(3-sqrt(5),0)=(sqrt(5),2)` vector director `(-2,sqrt(5))`, pendent `m=-sqrt(5)/2`.

    L'equació de la recta (punt pendent) és:

    `y=-sqrt(5)/2(x-3+sqrt(5))`


    I l'altre:


    `(3,2)-(3+sqrt(5),0)=(-sqrt(5),2)` vector director `(2,sqrt(5))`, pendent `m=sqrt(5)/2`.

    L'equació de la recta (punt pendent) és: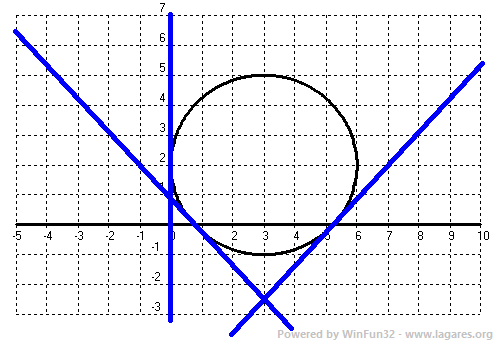

    `y=sqrt(5)/2(x-3-sqrt(5))`