|
7-Dibuixa la circumferència `x^2+y^2+6x-6y+9=0`. Calcula la potència del punt `P(3,1)` i la posició respecte al circumferència. Troba el punt més proper i llunya a `P` de la circumferència. SOLUCIÓ:
Potència `3^2+1^2+6·3-6·1+9 = 31 > 0 =>` exterior. Per trobar el punt més proper i el més llunyà calcularem les interseccions entre la circumferència i la recta que passa pel punt exterior `(3,1)` i el seu centre `(-3,3)`. Vector director `= (3,1)-(-3,3)=(6,-2) =>` associat `= (1,3)`. Recta `x+3y+c=0` substituim pel punt `(3,1)`, `3+3+c=0 => c = -6`. Equació `x+3y-6=0` Resolem el sistema:
`x^2+y^2+6x-6y+9=0` `x=6-3y` `x^2+y^2+6x-6y+9=0` `(6-3y)^2+y^2+6(6-3y)-6y+9=0` `36-36y+9y^2+y^2+36-18y-6y+9=0` `10y^2-60y+81=0` `y_1= 3+3/sqrt(10) => x_1=-3-9/sqrt(10)` 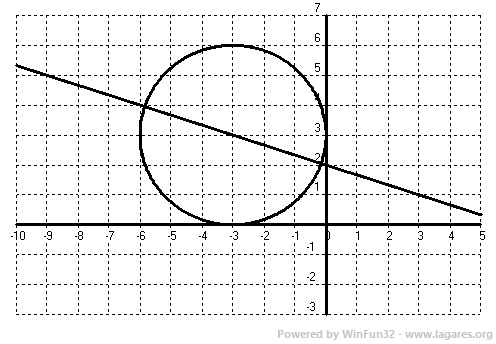 |