|
5-Sabem que una circumferència passa pel punt `(3,-1)` i és tangent a la recta `y=x+1` en el punt d'abscissa `3`. Calcula la seva equació. SOLUCIÓ:
El centre estarà en la recta perpendicular a la recta `y=x+1` que passa pel punt `(3,4)` `y=x+1` equació general `-x+y-1=0` vector associat `(-1,1)` vol dir que l'associat a la recta perpendicular és `(1,1)`. Equació de la perpendicular `x+y+c=0` Per trobar la `c` substituim pel punt `(3,4)`, `3+4+c=0 => c=-7` o sigui el centre es troba en la recta `x+y-7=0` Per trobar el centre podem fer la intersecció de la recta anterior amb la mediatriu dels dos punts `(3,-1)` i `(3,4)` Per trobar l'equació de la mediatriu busquem el punt mig dels dos punts `= ((3,4)+(3,-1))/2 = (3,3/2)` I el vector associat de la recta buscada és el vector que va d'un punt a l'altre, `(3,4)-(3,-1)=(0,5)` O sigui l'equació de la mediatriu dels dos punts és `0x+5y+c=0` substituin pel punt mig `(3,3/2) => 5·3/2+c=0 => c=-15/2`. L'equació de la mediatriu és `5y-15/2=0 => y-3/2=0 => y=3/2` Cal trobar la intersecció entre les dues rectes: `y=3/2` i `x+y-7=0`. Substituint `x+3/2-7=0 => x=11/2`. El centre es troba en el punt `(11/2,3/2)` Per trobar el radi cal buscar el módul del vector que va del centre a qualsevol dels dos punts, per exemple el `(3,4)`, `(11/2,3/2)-(3,4) = (5/2,-5/2)`, mòdul `= sqrt((5/2)^2+(-5/2)^2)= 5/sqrt(2)` Finalment l'equació de la circumferència de centre `(11/2,3/2)` i radi `5/sqrt(2)` queda: 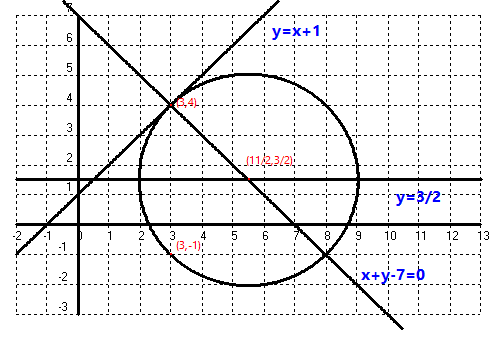 |