|
1-Esbrina si els punts `P(1,2)`, `Q(2,1)` i `R(0,0)` se situen en la mateixa circunferència. Si és així, troben l'equació. SOLUCIÓ: a) No formaran part de la mateixa circumferència si no estan alineats. Per la qual cosa agafem els vectors `RP=(1,2)` i `RQ=(2,1)` i veiem que no són proporcionals. `2/1\ne1/2` b) Per trobar el centre el que farem és calcular la intersecció entre dues mediatrius. i) La que passa per `R` i `P`: Vector associat `(1,2)`. Passa pel punt mig, `(1/2,2/2)=(1/2,1)`. `x+2y+c=0` `1/2+2+c=0 => c=-5/2` `x+2y-5/2=0 => 2x+4y-5=0` ii) la que passa per `R` i `Q`: Vector associat (2,1). Passa pel punt mig, `(2/2,1/2)=(1,1/2)`. `2x+y+c=0` `2+1/2+c=0 => c=-5/2` `2x+y-5/2=0 => 4x+2y-5=0` Per trobar el centre cal resoldre el sistema de les dues rectes: `2x+4y-5=0` `4x+2y-5=0` `x=5/6` i `y=5/6` Centre `(5/6,5/6)` c) Per trobar el radi buscarem el mòdul del vector que va del centre a un dels punts: Vector `CR=(5/6,5/6)`, mòdul `= sqrt((5/6)^2+(5/6)^2)=sqrt(50/36)=sqrt(25/18)` d) Finalment amb el centre i el radi tenim l'equació de la circumferència: `(x-5/6)^2+(y-5/6)^2=25/18` 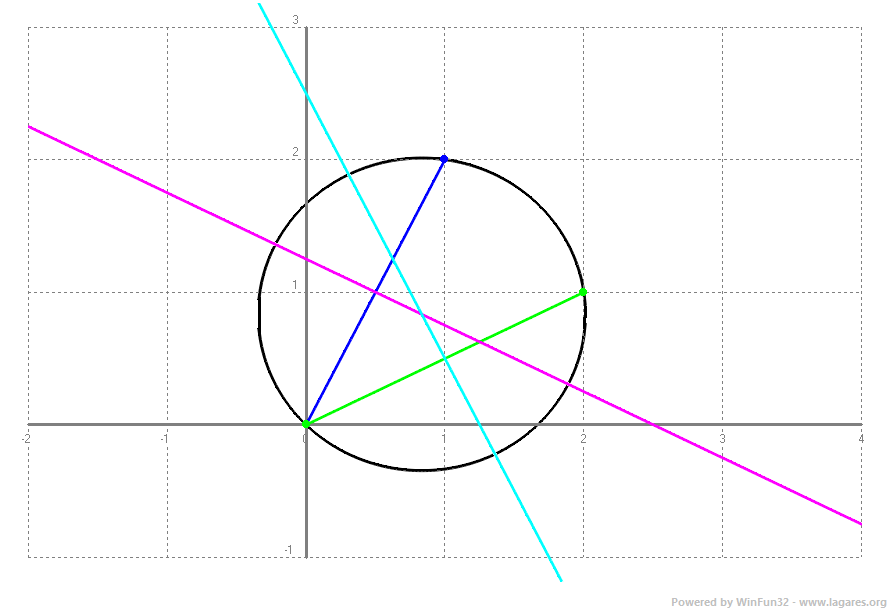 |